Learning Python with Advent of Code Walkthroughs
Dazbo's Advent of Code solutions, written in Python
The Python Journey - Shortest Path Algorithms - BFS, Dijkstra, and A*
Useful Links
Graphs and Graph TheoryNetworkXA* AlgorithmHeapqRecursion
Page Contents
- Overview
- Algorithm Summary
- The Final Frontier!
- Breadth First Search (BFS)
- Dijkstra’s Algorithm
- A* Algorithm
- Credit Where It’s Due
Overview
These algorithms help you find optimum paths through a graph.
Honestly, you won’t get far in Advent-of-Code if you don’t know them. Eric loves challenges like…
- Find the shortest path from a to b
- Find the optimum way to arrange this thing
Here are my three top reasons why you should learn this:
- You’ll get the right answer!
- It’ll save you LOADS of time and effort.
- These algorithms are cool!!
Algorithm Summary
First, let me provide a quick summary and comparison. Then we’ll get into the details after.
| Algorithm | Summary | When To Use It |
|---|---|---|
| Breadth First Search (BFS) | Aka "flood fill". Explores equally in all directions. Uses a FIFO queue.
A list will work,
but a deque is best. |
For finding the shortest path where the _cost_ is constant for any move. Or, for finding every point in a graph. Or for finding ALL paths from a to b. |
| Dijkstra’s Algorithm | Flood fill + a cost-based optimisation. I.e. prioritises paths to explore, favouring lower cost paths. Uses a _priority queue_, i.e. heapq. |
When movement costs may vary. |
| A* | Optimised for a single destination. I.e. prioritises paths that _seem_ to be approaching the goal. Still uses a heapq, but uses some sort of cost heuristic. Depending on the value of the distance heuristic, it may not add much value over Dijkstra, and may actually be slower. |
When we have an idea of the direction we need to follow. |
The Final Frontier!
All these algorithms utilise the concept of an expanding frontier. This expanding frontier is sometimes called a flood fill. It gives us a way to visit every allowed location on a map.
How the frontier works:
- Pick and remove a location from the frontier. Let’s call it current.
- Expand the frontier by finding all of the valid next moves from current. Let’s call them neighbours. Add the neighbours to the frontier.
Here’s some code that will perform a flood fill to explore every valid location in the graph:
frontier = Queue() # For BFS, we just use a FIFO queue.
frontier.append(start)
explored = set() # To stop us exploring the same location more than once.
explored.add(start)
# keep going until the frontier is empty; i.e. when we've explored all the valid nodes
while frontier:
current = frontier.popleft() # pop the first item off the FIFO queue
for next in graph.neighbors(current): # get all the valid neighbours
if next not in explored:
frontier.append(next) # add it to the frontier
explored.add(next) # mark it as explored
Breadth First Search (BFS)
BFS can be used to find a path from a to b. It can also be used to find paths from a to all locations in the graph.
It is guaranteed to find a solution if one exists. The frontier expands at an equal rate in all directions, and uses a FIFO (first-in, first-out) queue to implement the frontier.
How It Works
- We want to explore a graph, made up of edges connected by vertices. E.g. if we’re solving the path through a map, then each map location is a vertex. The graph has a start location, which is the root node of our tree. So we add the root to the frontier.
- It then explores all adjacent nodes. These will be
distance=1from the root. We add those to the frontier. - Then we explore all the nodes that are adjacent to those nodes. I.e. the nodes that are
distance=2from the root. - The BFS algorithm ensures that the same vertex is not followed twice; i.e. we never revisit a node we’ve visited before. This is crucial because it means that once we’ve a path to a note, we must have found the shortest route to that node.
So the sequence of exploration looks like this:
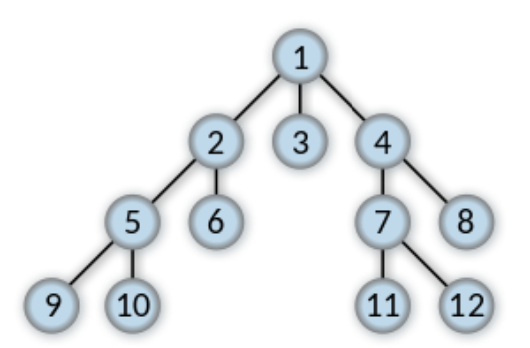
The numbers represent the sequence of traversal. But note that it is possible for the same node to appear in the tree more than once.
When we find a node that matches our goal, we stop. Thus, a BFS is just a flood fill, with a goal.
The Queue
We can implement the queue in many ways:
- Using a vanilla
list. - Better: using a
dequeto implement a FIFO queue; it is much more efficient for appending and popping at each end. - If we use a
heapq, then we end up popping based on a priority rather than FIFO. This is how we implement Dijkstra’s Algorithm or A*. - If we use a
stack, then we end up with last-in, first-out (LIFO), which actually turns a BFS into a depth first search (DFS)!- (Aside: You can also implement DFS using recursion, where the “stack” is just the program’s own call stack. This is often cleaner for tree-like problems!)
Implementing the BFS
Here’s some pseudocode that shows how to implement the BFS:
function BFS(graph, root):
queue = new Queue()
label root as explored # we know about this node, but not its children
queue.enqueue(root)
while queue not empty:
current = queue.pop()
if current is goal:
return current
for neighbour in graph.adjacent_nodes(current):
if neighbour is not explored:
label neighbour as explored
queue.enqueue(neighbour)
There are a couple of convenient ways to label a node as explored:
- We can store them in a
set. - We can add them to a
dictionary
If we use a set:
frontier = deque() # For BFS, we need a FIFO queue. A deque is perfect.
frontier.append(start)
explored = set() # To stop us exploring the same location more than once.
explored.add(start)
# keep going until the frontier is empty; i.e. when we've explored all the valid nodes
while frontier:
current = frontier.popleft() # pop the first item off the FIFO queue
if current == goal:
break
for next in graph.neighbors(current): # get all the valid neighbours
if next not in explored:
frontier.append(next) # add it to the frontier
explored.add(next) # mark it as explored
if current != goal:
# there was no solution!
Keeping Track of Distance
If we’re only interested in the shortest distance to a point, but we don’t need to create the actual path, a cool trick is to keep track of the distance in our queue. E.g.
frontier = deque() # For BFS, we need a FIFO queue. A deque is perfect.
frontier.append(start, 0) # Queue always includes (point, steps)
explored = set() # To stop us exploring the same location more than once.
explored.add(start)
# keep going until the frontier is empty; i.e. when we've explored all the valid nodes
while frontier:
current, steps = frontier.popleft() # pop the first item off the FIFO queue
if current == goal:
break
for next in graph.neighbors(current): # get all the valid neighbours
if next not in explored:
frontier.append(next, steps+1) # add it to the frontier
explored.add(next) # mark it as explored
if current != goal:
# there was no solution!
# distance from start to goal = steps
Breadcrumb Trail
If we use a dictionary instead of a set, we can create a breadcrumb trail to each point we’ve explored.
Let’s explore every valid point in the graph:
frontier = deque() # For BFS, we just use a FIFO queue. A deque is perfect.
frontier.append(start)
came_from = {} # To stop us exploring the same location more than once; and for breadcrumbs
came_from[start] = None # This marks the last breadcrumb
# keep going until the frontier is empty; i.e. when we've explored all the valid nodes
while frontier:
current = frontier.popleft() # pop the first item off the FIFO queue
for next in graph.neighbors(current): # get all the valid neighbours
if next not in came_from:
frontier.append(next) # add it to the frontier
came_from[next] = current
We can then create the breadcrumb path, like this:
current = goal # start at the end
path = [] # to store every point in a specific path
while current != start:
path.append(current)
current = came_from[current] # get the next node in the trail
path.append(start) # optional - depends if we want the first node to be included or not
path.reverse() # optional - depends whether we want start->end or end->start
BFS Examples
- Lava basins flood fill with BFS - 2021 Day 9
- Cave navigating with BFS and allowing repeats - 2021 Day 12
- Cave navigating with BFS and NetworkX - 2021 Day 12
- Path through a map with elevation, plus breadcrumb trail - 2022 Day 12
- BFS path to outside - 2022 Day 18
- BFS with class generating next states - 2022 Day 24
- Branching paths through a grid of mirrors - 2023 Day 16
- BFS with backtracking, to find number of locations we can reach in n steps - 2023 Day 21
- Standard BFS with explored set to handle merging beams - 2025 Day 7
- BFS to find connected components (circuits) - 2025 Day 8
Dijkstra’s Algorithm
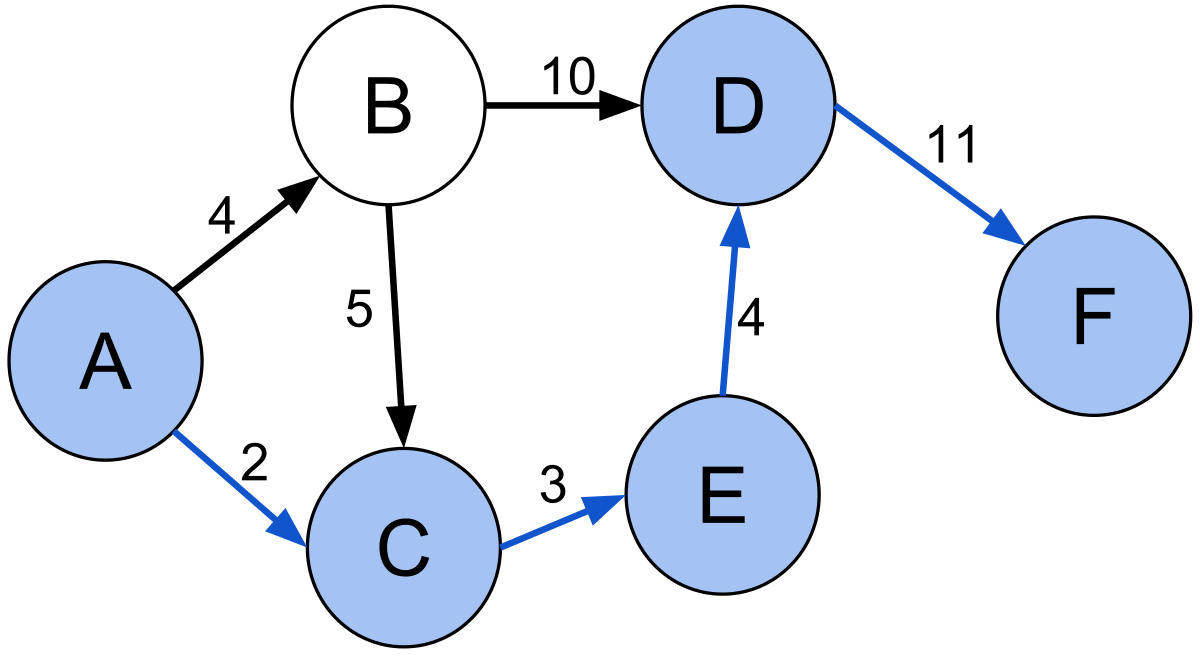
This algorithm is like BFS. But instead of expanding the frontier in all directions with equal weight - called an unweighted pathfinder algorithm - we instead prioritise popping the node that has the lowest overall cost.
Dijkstra’s algorithm is perfect for:
- Finding the best path through a graph, when the edges of the graph have different weights.
- Finding the shortest path to every node for any given node.
How It Works
- The frontier is implemented using a priority queue, which we implement using a
heapq. Theheapqdata structure allows us to efficiently pop the item with the lowest priotity. - Our starting node will have a cumulative cost of 0.
- For each valid adjacent node, we store this node along with the cumulative cost so far. This is given by the previous cost, plus the cost of this particular edge. This differs from BFS, since in BFS the cost is always constant for every adjacent node.
- In BFS, we check for duplicates when we insert. But in Dijkstra’s, if we arrive at a node we’ve arrived at before, then we can skip it if the current cumulative cost is higher than the previous cost to reach this node. I.e. for each node, always store the minimum cost to reach it.
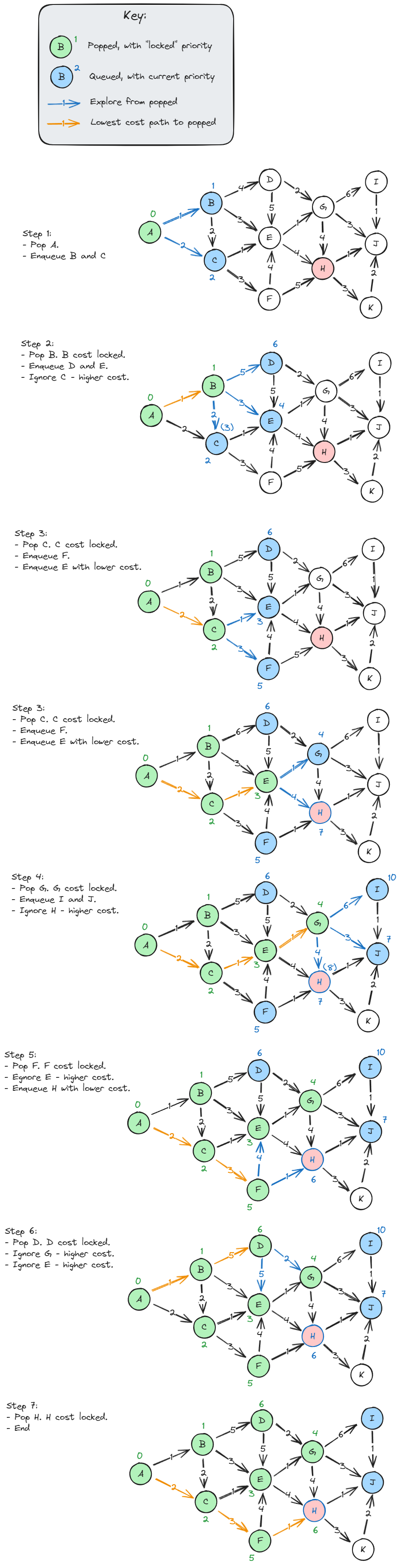
- In BFS, we typically end when we reach the goal. I.e. because if we’ve reached the goal, we must have taken the minimum number of steps to get to it. But in Dijkstra’s algorithm, there may be different ways to reach the goal, and they may have different costs. So we only end when we pop the goal off the priority queue. Because once we pop the goal, then we know we’ve popped it with the minimum possible cumulative cost.
Check out the illustration below, that shows how the algorithm finds our goal, H:
Dijkstra’s Algorithm Examples
- Risk maze - with heapq and breadcrumbs - 2021 day 15
- Lowest cost rearranging amphipods - with next state, heapq and breadcrumbs - 2021 day 23
- Hill climbing with NetworkX - 2022 Day 12
- Lowest cost path with turning constraints - 2023 Day 17
- Dijkstra to find lowest cost path - 2023 Day 17
- Finding shortest path through a maze where turns have different cost - 2024 Day 16
A* Algorithm
The A* Algorithm is a lot like BFS. But instead of expanding frontier in all directions equally - called an unweighted pathfinder algorithm - we prioritise popping from the frontier in the direction that we believe takes us closer to our goal. Thus, a weighted pathfinder algorithm.
To do this, we need two key changes, compared to the BFS:
- We need to use a
heapq. Recall that aheapqallows us to pop elements based on a priority. - We need to provide a heuristic function, i.e. a function that computes some sort of cost. The heuristic estimates the cost to get from any given node to the goal. This cost is used to determine the priority. Typically, the heuristic will be a function that estimates distance, such as a Manhattan distance function.
So, an A* implementation requires the combination of:
- Cost of the path from the start point to the current point (e.g. steps so far)
- A heuristic estimation of the cost for the current point to the end piont (e.g. Manhattan distance)
We need both, because if we only include the distance heuristic, then we end up with a greedy BFS which tries to get closer to the goal without considering the path cost so far.
Turning a BFS into an A*
Here’s a BFS that creates a breadcrumb path. The priority of the pop is simply the number of steps taken from the starting point.
def solve_with_bfs(start:Point, goal:Point) -> tuple[int, dict]:
queue = []
heapq.heappush(queue, (0, start)) # posn, steps
came_from = {} # use a dict so we can build a breadcrumb trail
came_from[start] = None
while queue:
step_count, curr_posn = heapq.heappop(queue)
# Check if the target is reached
if curr_posn == goal:
return step_count, came_from
# Explore adjacent hexagons
for dx, dy in Hex.hex_vectors.values():
adjacent = curr_posn + Point(dx, dy)
if adjacent not in came_from:
came_from[adjacent] = curr_posn
heapq.heappush(queue, (step_count + 1, adjacent))
assert False, "We should never get here."
Here I’ve changed the code to an A*. Now I’m popping from the heapq, using a priority that is sum of the number of steps taken, and the estimated distance to the goal.
def solve_with_astar(start: Point, goal: Point) -> tuple[int, dict]:
""" Obtain the fastest path from origin to goal using A*.
Returns: tuple[int, dict]: steps required, breadcrumbs
"""
queue = []
came_from = {} # use a dict so we can build a breadcrumb trail
came_from[start] = None
heapq.heappush(queue, (0, 0, start)) # distance heuristic, steps, posn
while queue:
_, step_count, curr_posn = heapq.heappop(queue)
# Check if the target is reached
if curr_posn == goal:
return step_count, came_from
# Explore adjacent hexagons
for dx, dy in Hex.hex_vectors.values():
adjacent = curr_posn + Point(dx, dy)
if adjacent not in came_from:
came_from[adjacent] = curr_posn
heuristic_cost = Hex.distance(adjacent, goal)
new_cost = step_count + 1 + heuristic_cost # heuristic is combination of distance to goal, and step count
heapq.heappush(queue, (new_cost, step_count + 1, adjacent))
assert False, "We should never get here."
I compared these two solutions when solving 2017 day 11. The BFS took 30 seconds, and the A* took just 20ms!!
A* Examples
Credit Where It’s Due
When I first learned these algorithms, the best guide I came across was this one. I wrote a lot of notes when I first read it, and in writing this page today, I’ve been referring to my previous notes. So, the content I’ve written here will likely have a lot in common with the amazing content from https://www.redblobgames.com.