Learning Python with Advent of Code Walkthroughs
Dazbo's Advent of Code solutions, written in Python

Advent of Code 2022 - Day 12
Day 12: Hill Climbing Algorithm
Useful Links
Concepts and Packages Demonstrated
BFS and Path AlgorithmsComprehensionClassesMatplotlib
Page Navigation
Problem Intro
About this time every year, we find AoC starts to itensify. And sometimes you get a problem where you either:
- just know how to do it, and it’s easy.
- have no idea, and it’s a nightmare.
For me, yesterday was a bit of a nightmare. But today was a relief because I do like a BFS problem!! A couple of years ago, I didn’t know my way around path-solving algorithms, and a problem like this one would have taken me forever. So it’s quite satisfying to be able to deploy knowledge acquired as a result of previous time and effort.
If you don’t know anything about algorithms like BFS, Dijkstra’s, and A*, then YOU NEED TO LOOK AT MY GUIDE. Honestly, it will totally change AoC experience!
Okay, so today’s problem…
Our input is a grid of elevation data. Elevation is represented by a-z,
where a is the lowest possible elevation, and z is the higest possible elevation.
The input data looks like this:
Sabqponm
abcryxxl
accszExk
acctuvwj
abdefghi
S is our start position and E is our goal.
From S, we can move to any adjacent position by moving left, right, up, or down; but only if the adjacent position’s elevation is less than or equal to: our current elevation, plus 1.
Part 1
What is the fewest steps required to move from your current position to the location that should get the best signal?
This is a pretty simple BFS!! Check my guide for how BFS works.
First, a bit of importing, and a Point class:
from __future__ import annotations
from collections import deque
from copy import deepcopy
from dataclasses import dataclass
from pathlib import Path
import time
SCRIPT_DIR = Path(__file__).parent
# INPUT_FILE = Path(SCRIPT_DIR, "input/sample_input.txt")
INPUT_FILE = Path(SCRIPT_DIR, "input/input.txt")
@dataclass(frozen=True)
class Point():
""" Point class, which knows how to return a list of all adjacent coordinates """
x: int
y: int
def neighbours(self) -> list[Point]:
""" Return all adjacent orthogonal (not diagonal) Points """
return [Point(self.x+dx, self.y+dy) for dx in range(-1, 2)
for dy in range(-1, 2)
if abs(dy) != abs(dx)]
Note that this Point class is able to return a list of all its neighbours. It does this with a list comprehension.
Next, our Grid class:
class Grid():
""" 2D grid of point values. """
def __init__(self, grid_array: list[str]) -> None:
""" Generate Grid instance from 2D array.
This works on a deep copy of the input data, so as not to mutate the input. """
self.array = deepcopy(grid_array) # Store a deep copy of input data
self.x_size = len(self.array[0])
self.y_size = len(self.array)
self.start = self._get_point_for_elevation("S")
self.goal = self._get_point_for_elevation("E")
def _all_points(self) -> list[Point]:
points = [Point(x, y) for x in range(self.x_size) for y in range(self.y_size)]
return points
def _get_point_for_elevation(self, x: str) -> Point:
""" Use this to find the point where "S" or "E" are located. """
assert x in ("S", "E"), "Specified point must be Start or End!"
for row_num, row in enumerate(self.array):
if x in row:
return Point(row.index(x), row_num)
def elevation_at_point(self, point: Point) -> int:
""" Elevation value at this point """
if point not in (self.start, self.goal):
return ord(self.array[point.y][point.x])
if point == self.start:
return ord("a") # we're told start location is elevation a
if point == self.goal:
return ord("z") # we're told start location is elevation z
def _point_in_grid(self, point: Point) -> bool:
""" Check if a location is within the grid """
if (0 <= point.x < self.x_size and 0 <= point.y < self.y_size):
return True
return False
def _valid_neighbours(self, location:Point):
""" Yield adjacent neighbour points.
We can move L, R, U, D by one unit. But we can only move to locations that
are no more than one higher than current elevation. """
current_elevation = self.elevation_at_point(location)
for neighbour in location.neighbours():
if self._point_in_grid(neighbour):
if self.elevation_at_point(neighbour) <= current_elevation + 1:
yield neighbour
def get_path(self, start: Point):
""" Given a start point, determine best path to reach the goal specified by 'E'.
Returns: list of points that make up the path
or: None, if no valid path from this start point.
"""
points_to_assess: deque[Point] = deque() # Points we want to get value of, and get neighbours for
points_to_assess.append(start) # where we start
came_from = {}
came_from[start] = None
while points_to_assess: # They should only ever be valid points
current = points_to_assess.popleft()
if current == self.goal: # We've reached the end
break
for neighbour in self._valid_neighbours(current):
if neighbour not in came_from: # We will need to assess this point
points_to_assess.append(neighbour)
came_from[neighbour] = current
# build the breadcrumb path
current = self.goal
path = []
while current != start:
path.append(current)
current = came_from[current]
return path
def __repr__(self) -> str:
return "\n".join("".join(map(str, row)) for row in self.array)
A few points about the above code:
_point_in_grid()is used to check if a point is within the grid._valid_neighbours()iterates through the neighbours of our point, and checks whether this neighbour is valid, given the rules about elevation.get_path()works by:- Performing a BFS from
StoE. - Uses a
dictionaryto explore the explored points, and to build the breadcrumb trail.
- Performing a BFS from
Now we solve as follows:
def main():
with open(INPUT_FILE, mode="rt") as f:
data = f.read().splitlines()
grid = Grid(data)
# Part 1
path = grid.get_path(grid.start)
p1_length = len(path)
print(f"Part 1: {p1_length}")
if __name__ == "__main__":
t1 = time.perf_counter()
main()
t2 = time.perf_counter()
print(f"Execution time: {t2 - t1:0.4f} seconds")
Easy when you know how!
Part 2
What is the fewest steps required to move starting from any square with elevation a to the location that should get the best signal?
“Oh awesome!”, I thought to myself. All I need to do is:
- Get a list of all the points with elevation
a. - Perform exactly the same BFS, but using each new start location, rather than
S.
So, that’s what I did. It worked straight away with the sample code. And then throw an exception with the real data. Doh!!
It turns out there’s a small gotcha, which took me quite a few minutes to debug. It turns out that many of the a start locations in the real data DO NOT HAVE SOLUTIONS. So we need to handle that situation.
Here are my changes to solve this part…
First, we add this method to our Grid class:
def all_lowest_elevation_points(self) -> set[Point]:
low_points = {point for point in self._all_points()
if self.array[point.y][point.x] == "a"
or self.array[point.y][point.x] == "S"}
return low_points
Then we need to handle the “no solution” scenario. We just add this code in the get_path() method,
before building our breadcrumbs.
if current != self.goal:
return None # No valid path from this point
Then we just add this to our main() method:
# Part 2
start_points = grid.all_lowest_elevation_points()
p2_length = p1_length
for start in start_points:
path = grid.get_path(start)
if path:
p2_length = min(p2_length, len(path))
print(f"Part 2: {p2_length}")
Results
The final code:
from __future__ import annotations
from collections import deque
from copy import deepcopy
from dataclasses import dataclass
from pathlib import Path
import time
SCRIPT_DIR = Path(__file__).parent
# INPUT_FILE = Path(SCRIPT_DIR, "input/sample_input.txt")
INPUT_FILE = Path(SCRIPT_DIR, "input/input.txt")
@dataclass(frozen=True)
class Point():
""" Point class, which knows how to return a list of all adjacent coordinates """
x: int
y: int
def neighbours(self) -> list[Point]:
""" Return all adjacent orthogonal (not diagonal) Points """
return [Point(self.x+dx, self.y+dy) for dx in range(-1, 2)
for dy in range(-1, 2)
if abs(dy) != abs(dx)]
class Grid():
""" 2D grid of point values. """
def __init__(self, grid_array: list[str]) -> None:
""" Generate Grid instance from 2D array.
This works on a deep copy of the input data, so as not to mutate the input. """
self.array = deepcopy(grid_array) # Store a deep copy of input data
self.x_size = len(self.array[0])
self.y_size = len(self.array)
self.start = self._get_point_for_elevation("S")
self.goal = self._get_point_for_elevation("E")
def _all_points(self) -> list[Point]:
points = [Point(x, y) for x in range(self.x_size) for y in range(self.y_size)]
return points
def all_lowest_elevation_points(self) -> set[Point]:
low_points = {point for point in self._all_points()
if self.array[point.y][point.x] == "a"
or self.array[point.y][point.x] == "S"}
return low_points
def _get_point_for_elevation(self, x: str) -> Point:
""" Use this to find the point where "S" or "E" are located. """
assert x in ("S", "E"), "Specified point must be Start or End!"
for row_num, row in enumerate(self.array):
if x in row:
return Point(row.index(x), row_num)
def elevation_at_point(self, point: Point) -> int:
""" Elevation value at this point """
if point not in (self.start, self.goal):
return ord(self.array[point.y][point.x])
if point == self.start:
return ord("a") # we're told start location is elevation a
if point == self.goal:
return ord("z") # we're told start location is elevation z
def _point_in_grid(self, point: Point) -> bool:
""" Check if a location is within the grid """
if (0 <= point.x < self.x_size and 0 <= point.y < self.y_size):
return True
return False
def _valid_neighbours(self, location:Point):
""" Yield adjacent neighbour points.
We can move L, R, U, D by one unit. But we can only move to locations that
are no more than one higher than current elevation. """
current_elevation = self.elevation_at_point(location)
for neighbour in location.neighbours():
if self._point_in_grid(neighbour):
if self.elevation_at_point(neighbour) <= current_elevation + 1:
yield neighbour
def get_path(self, start: Point):
""" Given a start point, determine best path to reach the goal specified by 'E'.
Returns: list of points that make up the path
or: None, if no valid path from this start point.
"""
points_to_assess: deque[Point] = deque() # Points we want to get value of, and get neighbours for
points_to_assess.append(start) # where we start
came_from = {}
came_from[start] = None
while points_to_assess: # They should only ever be valid points
current = points_to_assess.popleft()
if current == self.goal: # We've reached the end
break
for neighbour in self._valid_neighbours(current):
if neighbour not in came_from: # We will need to assess this point
points_to_assess.append(neighbour)
came_from[neighbour] = current
if current != self.goal:
return None # No valid path from this point
# build the breadcrumb path
current = self.goal
path = []
while current != start:
path.append(current)
current = came_from[current]
return path
def __repr__(self) -> str:
return "\n".join("".join(map(str, row)) for row in self.array)
def main():
with open(INPUT_FILE, mode="rt") as f:
data = f.read().splitlines()
grid = Grid(data)
# Part 1
path = grid.get_path(grid.start)
p1_length = len(path)
print(f"Part 1: {p1_length}")
# Part 2
start_points = grid.all_lowest_elevation_points()
p2_length = p1_length
for start in start_points:
path = grid.get_path(start)
if path:
p2_length = min(p2_length, len(path))
print(f"Part 2: {p2_length}")
if __name__ == "__main__":
t1 = time.perf_counter()
main()
t2 = time.perf_counter()
print(f"Execution time: {t2 - t1:0.4f} seconds")
And the output looks like this:
Part 1: 472
Part 2: 465
Execution time: 4.0638 seconds
Optimisations
In retrospect, it was really dumb for me to solve Part 2 but running a BFS for EVERY a location. It would be much faster to run the BFS once, storing the path from the E to every a. Then we can simply print the lengths of the valid paths to each a.
So here’s the amended code:
SCRIPT_DIR = Path(__file__).parent
# INPUT_FILE = Path(SCRIPT_DIR, "input/sample_input.txt")
INPUT_FILE = Path(SCRIPT_DIR, "input/input.txt")
@dataclass(frozen=True)
class Point():
""" Point class, which knows how to return a list of all adjacent coordinates """
x: int
y: int
def neighbours(self) -> list[Point]:
""" Return all adjacent orthogonal (not diagonal) Points """
return [Point(self.x+dx, self.y+dy) for dx in range(-1, 2)
for dy in range(-1, 2)
if abs(dy) != abs(dx)]
class Grid():
""" 2D grid of point values. """
def __init__(self, grid_array: list[str]) -> None:
""" Generate Grid instance from 2D array.
This works on a deep copy of the input data, so as not to mutate the input. """
self.array = grid_array # Store a deep copy of input data
self.x_size = len(self.array[0])
self.y_size = len(self.array)
self.start = self._get_point_for_elevation("S")
self.goal = self._get_point_for_elevation("E")
def _all_points(self) -> list[Point]:
points = [Point(x, y) for x in range(self.x_size) for y in range(self.y_size)]
return points
def all_lowest_elevation_points(self) -> set[Point]:
low_points = {point for point in self._all_points()
if self.array[point.y][point.x] == "a"
or self.array[point.y][point.x] == "S"}
return low_points
def _get_point_for_elevation(self, x: str) -> Point:
""" Use this to find the point where "S" or "E" are located. """
assert x in ("S", "E"), "Specified point must be Start or End!"
for row_num, row in enumerate(self.array):
if x in row:
return Point(row.index(x), row_num)
def elevation_at_point(self, point: Point) -> int:
""" Elevation value at this point """
if point not in (self.start, self.goal):
return ord(self.array[point.y][point.x])
if point == self.start:
return ord("a") # we're told start location is elevation a
if point == self.goal:
return ord("z") # we're told start location is elevation z
def _point_in_grid(self, point: Point) -> bool:
""" Check if a location is within the grid """
if (0 <= point.x < self.x_size and 0 <= point.y < self.y_size):
return True
return False
def _valid_neighbours(self, location:Point):
""" Yield adjacent neighbour points.
We can move L, R, U, D by one unit. But we can only move to locations that
are no more than one higher than current elevation. """
current_elevation = self.elevation_at_point(location)
for neighbour in location.neighbours():
if self._point_in_grid(neighbour):
if self.elevation_at_point(neighbour) <= current_elevation + 1:
yield neighbour
def get_breadcrumbs(self, end: Point) -> dict[Point, Point]:
""" Given the start point, find all paths to destination. """
points_to_assess: deque[Point] = deque() # Points we want to get value of, and get neighbours for
points_to_assess.append(end) # where we start
came_from = {}
came_from[end] = None
# BFS with no goal
while points_to_assess: # They should only ever be valid points
current = points_to_assess.popleft()
for neighbour in self._valid_neighbours(current):
if neighbour not in came_from: # We will need to assess this point
points_to_assess.append(neighbour)
came_from[neighbour] = current
return came_from
@staticmethod
def create_path(breadcrumbs: dict[Point, Point], start: Point, goal: Point):
""" Calculate the path from goal to start, as list of Points.
Return None if no valid path. """
path = []
current = goal # we need to walk backwards from destination to start
while current != start:
path.append(current)
if current in breadcrumbs:
current = breadcrumbs[current]
else:
return None
return path
def __repr__(self) -> str:
return "\n".join("".join(map(str, row)) for row in self.array)
def main():
with open(INPUT_FILE, mode="rt") as f:
data = f.read().splitlines()
grid = Grid(data)
breadcrumbs = grid.get_breadcrumbs(grid.start) # every path to every point
# Part 1
path = grid.create_path(breadcrumbs, grid.start, grid.goal) # from 'S' to 'E'
print(f"Part 1: {len(path)}")
# Part 2
best_path = path
for goal in grid.all_lowest_elevation_points(): # Going to all 'a'
if goal in breadcrumbs:
path = grid.create_path(breadcrumbs, goal, grid.goal) # from 'a' to 'E'
if path:
if len(path) < len(best_path):
best_path = path
print(f"Part 2: {len(best_path)}")
if __name__ == "__main__":
t1 = time.perf_counter()
main()
t2 = time.perf_counter()
print(f"Execution time: {t2 - t1:0.4f} seconds")
It is indeed much faster!
Part 1: 472
Part 2: 465
Execution time: 0.3467 seconds
Visualisation
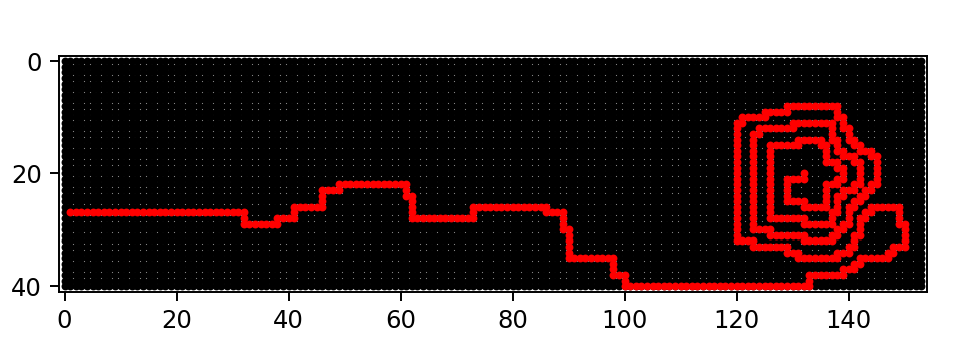
Let’s add a quick visualisation. It’s very easy. I just added this:
def render_as_plt(grid, path):
""" Render the display as a scatter plot """
x_vals = [point.x for point in grid.all_points()]
y_vals = [point.y for point in grid.all_points()]
path_x = [point.x for point in path]
path_y = [point.y for point in path]
axes = plt.gca()
axes.set_aspect('equal')
axes.set_xlim(min(x_vals)-1, max(x_vals)+1)
axes.set_ylim(min(y_vals)-1, max(y_vals)+1)
axes.invert_yaxis()
axes.scatter(x_vals, y_vals, marker="o", s=5, color="black")
axes.scatter(path_x, path_y, marker="o", s=5, color="red")
plt.show()
Here’s what it looks like: