Learning Python with Advent of Code Walkthroughs
Dazbo's Advent of Code solutions, written in Python
The Python Journey - Priority Queues and Heaps
Useful Links
Graphs and Graph TheoryheapqShortest Path Algorithms
Page Contents
Overview
Whilst the Python list is great for storing an arbitrary number of elements, and for being able to retrieve elements quickly by position, the list does not perform well when working with huge volumes of ordered data. For example, imagine we had a list with millions of objects in a random order, and we need to continually retrieve the object that is largest. In this situation, Python needs to continually scan the entire list to find the one that is largest. This is not an efficient approach!
And that’s where a priority queue comes in. A priority queue is an abstract dta structure designed to allow fast retrieval of the largest or smallest value, regardless of the number of items being stored.
When To Use a Priority Queue?
- If you need to work with unordered data, and you need to frequently retrieve an element by index, use a
list. - If you need to work with large volumes of data, and you want to be able to always retrieve the smallest or largest value - then use a priority queue.
Typical use cases for a priority queue are:
- Finding the shortest path, e.g. through a maze
- Merging large sets of sequenced data
- Scheduling based on priority
- Solving optimisation problems, i.e. find the most efficient way to do x.
Abstract Data Structure?
What does abstract data structure even mean? It means that however we implement this data structure, it needs to adhere to a few rules. A implementation for a priority queue should include these operations:
- Check if it is empty
- The ability to push (i.e. add) a new element
- The ability to pop (retrieve and remove) the element that is highest priority. Highest priority can mean whatever you want. For example, it might be the largest value; it might mean closeness to a goal. If you’ve implemented a priority queue that is returning the largest values, you can always make it return the smallest value by simply negating the value.
Heaps
Heaps are commonly used to implement priority queues in a manner where performance is guaranteed in relation to the size of the overall dta structure. This is possible because heaps implement a priority queue in the form of a binary tree.
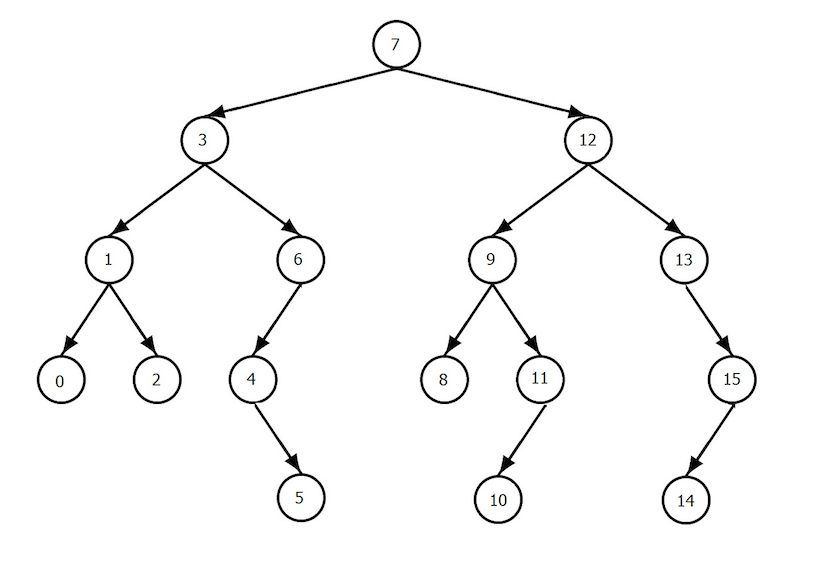
Recall from graphs that a tree is an acyclic graph - i.e. one in which no loops are created - where vertices are connected by exactly one path.
A heap has additional characteristics, called heap property:
- A node will have no more than two children. (A requirement of a binary tree.)
- All levels are full, with the exception of the deepest level, which may not yet be full.
- To ensure that the heap is able to pop highest priority, the heap property ensures that the value of a node is always smaller than both of its children.
- Popping will always return the smallest (highest priority) element.
- Pushing/popping temporarily violates the heap property, and then the heap restructures to restore the heap property. This will involve switching parents and children, as required.
The performance of pushing/popping a heap is guaranteed to be proportional to the base-2 log of the size of the queue.
Heapq
In Python, we have a ready-made heap available in the form of the heapq.
It is a complete binary tree implemented _on top of a list. For this reason, it is easy to convert an existing list or iterable to a heapq.
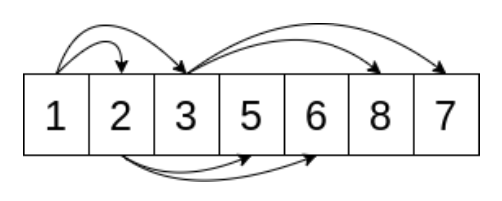
Recall that the heap property requires that a parent has a smaller value (higher priority) than both of its children. This is implemented in the heapq as shown below.

The arrows indicate the children of any given parent, and shows where the children are always located, in the heapq implementation.
The heapq pops based on the smallest value having the highest priority.
So, if we (say) store state objects in the queue, you could implement the __lt__() method of the state object such that a < b if a is closer to the goal.
Heapq Methods
heapq.heapify(some_iterable)heapq.heappush(queue, element)heapq.heappop(queue)heapq.heappushpop(heap, element)- more efficient if we need to both push and popheapq.merge(iterable1, iterable2, …)- merges sorted iterables and returns an iterator
Heapq Elements and Priority
Recall that the heapq always pops the item with the smallest value. Thus, highest priority = smallest value. Bear this in mind when adding objects to a heapq.
An alternative way to add things to a queue with our desired priority is to add them as the second element of a tuple. This is because if we add tuples to a heapq, the first item in the tuple is used for the priority.
E.g.
heapq.heappush(frontier, (priority, item))
We’ll look at some real heapq usage when we move on to look at Shortest Path Algorithms.