Learning Python with Advent of Code Walkthroughs
Dazbo's Advent of Code solutions, written in Python
The Python Journey - Graphs and Graph Theory

Useful Links
Graph Theory (Wikipedia)Graph Theory 101 (Harvard Uni)NetworkX
Page Contents
Graph Theory Overview
Here we’re talking about very specific definitions of a graph. Not the kind of graph where you plot points on x and y axes, but rather: an abstract model that represents a set of vertices (also called nodes or points), linked together by edges (also called links or lines).
Graph Types
Graphs can be categorised as:
- Undirected: edges have no direction; or directed: edges have direction.
- Unweighted: edges have no magnitude; or weighted: edges have magnitude.
We can summarise like this:
| Graph Type | Description | E.g. |
|---|---|---|
| Unweighted Undirected (“graph”) | An associated set of unordered nodes. | 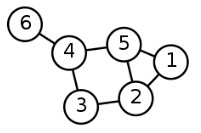 |
| Unweighted Directed (“digraph”) | An associated set of ordered nodes. It is the direction of the edges (arrows) that dictates order. | 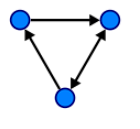 |
| Weighted Undirected (“weighted graph”) | The edges have magnitude, and this magnitude is important. E.g. the weight could represent distance, or cost. | 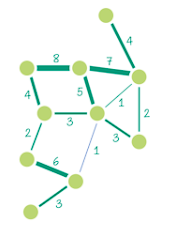 |
| Weighted Directed (“weighted digraph”) | The edges have both magnitude and direction. It is possible for A -> B to have a different magnitude from B -> A. | 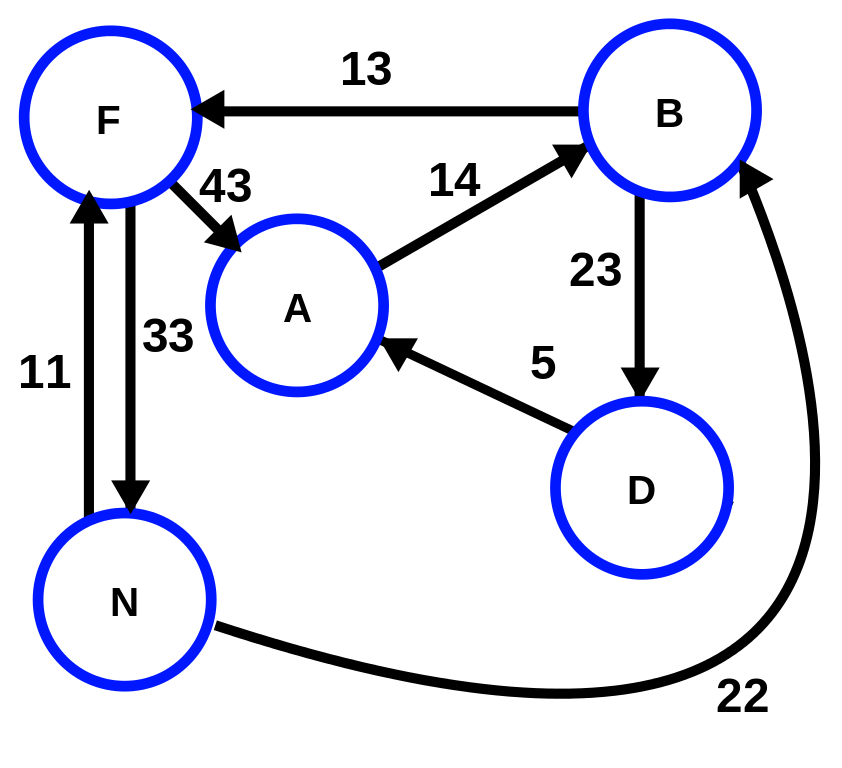 |
It’s worth noting that undirected graphs can be either unweighted and weighted; and directed graphs can be either unweighted or weightd.
Tree
A tree is an acyclic graph - i.e. one in which no loops are created - where vertices are connected by exactly one path.
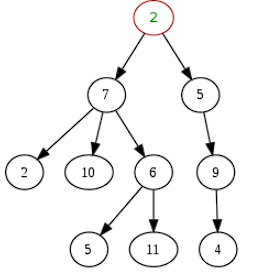
However, as the image shows, a given node can appear more than once in a tree.
Adjacency Lists
It’s generally a good idea to store graphs using adjacency lists. I.e. a map that links a given vertex to all the vertices it is directly connected to.
Consider the undirected graph above, where:
- 1 is connected to 2 and 5. (2 edges.)
- 2 is connected to 1, 3, and 5. (3 edges.)
- 3 is connected to 2 and 4. (2 edges.)
- 4 is connected to 3, 5, and 6. (3 edges.)
- 5 is connected to 1, 2, and 4. (3 edges.)
- 6 is connected to 4. (1 edge.)
Imagine that we’re not given the overall graph, but we’re instead only provided with individual edges. In this case, we can build the graph using an adjacency list as follows:
from collections import defaultdict
edges = set() # store edge edge as a tuple of (node_a, node_b)
# Imagine we're only provided with the edges.
edges.add((1, 2))
edges.add((1, 5))
edges.add((2, 1))
edges.add((2, 3))
edges.add((3, 2))
edges.add((3, 4))
edges.add((4, 3))
edges.add((4, 5))
edges.add((4, 6))
edges.add((5, 1))
edges.add((5, 2))
edges.add((5, 4))
edges.add((6, 4))
# Now we build the adjacency map
node_map = defaultdict(set) # Use a set in order to filter out duplicate connections
for x, y in edges:
node_map[x].add(y) # a list of vertices that link to x
node_map[y].add(x) # a list of vertices that link to y
for vertex, connections in node_map.items():
print(f"{vertex}: {connections}")
Output:
1: {2, 5}
2: {1, 3, 5}
3: {2, 4}
4: {3, 5, 6}
5: {1, 2, 4}
6: {4}
Note:
- When we have an unweighted graph and we only one to store which nodes are adjacent to another node, we can use a dict where the key is the node, and the values are the set of adjacent nodes.
- Where we have a weighted graph and we’re also interested in the magnitude of the edges, we can use a nested dictionary, where the outer key is the node, and the outer value is the inner dictionary. The inner dict uses adjacent nodes for keys, and edge manitudes for values.