Advent of Code 2022 - Day 8

Day 8: Treetop Tree House

Useful Links

‹›

Concepts and Packages Demonstrated

Class Dataclass List comprehension zip Working with images

Problem Intro
Part 1
Part 2
Results
Visualisation

Problem Intro

We’ve arrived at an area where tall trees are arranged in a rigid grid. The trees are of varying heights.

The locations and heights of the trees is given by our input data, which looks something like this:

Part 1

The elves want to determine if our input area provides sufficient tree cover. A tree in any given position is visible from outside the grid if:

The tree is on any edge.
The tree is taller than any trees between this tree and any edge.

How many trees are visible from outside the grid?

We’re told we only have to consider orthogonal directions, i.e. left, right, up and down. We don’t have to worry about diagonals.

Here’s my approach:

Create a Grid class to hold the locations and heights of the trees. Pass in the rows of int to create it.
Also store the data in columns, to make life easy.
Iterate through all trees in the grid.
- If this tree is on an edge, it is visible from the outside.
- If this tree is taller than any trees to the left, right, above or below (as seen in the map), it is visible from the outside. If so, it is visible.

Simple enough!

Let’s read in the data:

    with open(INPUT_FILE, mode="rt") as f:
        data = f.read().splitlines()
        
    rows = [[int(x) for x in row] for row in data]

Here I’m using a nested comprehension to get each row of numbers, and then for each row, to convert the number to an int.

Next, here is a class to represent any given 2D (x,y) Point. I’m using a dataclass. Nothing new to say about this.

@dataclass(frozen=True)
class Point():
    """ Point class """
    x: int
    y: int

Next, I create a Grid class. This is where all the good stuff happens…

class Grid():
    """ Represents a grid of trees heights """
    
    def __init__(self, grid_rows: list) -> None:
        """ Expects data in the format... [[3, 0, 3, 7, 3], [2, 5, 5, 1, 2], ...] """
        self.rows: list[list[int]] = grid_rows
        self.cols = list(zip(*self.rows))
        self._width = len(self.cols)
        self._height = len(self.rows)
        self.size = self._width * self._height
    
    def height_at_point(self, point: Point) -> int:
        return self.rows[point.y][point.x]

    def is_visible(self, point: Point) -> bool:
        """ A tree is visible if it is on any edge, 
        or if there are no taller trees in the same row or column. """
        
        # check if it's on an edge
        if point.x == 0 or point.x == self._width-1:
            return True
        if point.y == 0 or point.y == self._height-1:
            return True
        
        value = self.height_at_point(point)
        # Check if taller than any other tree in the row. If so, it is visible.
        if value > max(self.rows[point.y][0:point.x]): return True
        if value > max(self.rows[point.y][point.x+1:]): return True
        
        # Now check the column. 
        if value > max(self.cols[point.x][0:point.y]): return True
        if value > max(self.cols[point.x][point.y+1:]): return True
        
        return False
    
    def get_hidden_trees(self) -> set[Point]:
        """ Returns all locations where trees are hidden from view. """
        return {Point(x, y) for x in range(self._height)
                            for y in range(self._width)
                            if not self.is_visible(Point(x,y))}
    
    def __repr__(self):
        return (f"{self.__class__.__name__}" 
               + f"(size={self.size}, rows={len(self.rows)}, cols={len(self.cols)})")

The __init__() method:
- Takes our list of lists of int, and stores it in the self.rows property.
- Then uses zip to obtain a new list that represents the data as columns rather than rows.
- We store the width and height of the Grid, for convenience.
The height_at_point(self, point: Point) simply returns the value stored at the given location.
The is_visible() method:
- Checks whether the Point is on an edge, by first checking if its x component is equal to 0 or the width-1, and by then checking if its y component is equal to 0 or the height-1.
- Then retrieves the value (height) of our tree.
- Then checks whether our tree is taller than any tree to the left or right. I’m slicing to get left and right.
- Then checks whether our tree is taller than any tree above or below. I’m slicing to get above and below.
- If any of the conditions above are True, then this tree is visible.
The get_hidden_trees() method uses a multi-sequence set comprehension as a short hand for iterating through all x, then all y, and then checking whether the value at that location is visible, using hte is_visible() method that we previously defined.

I didn’t actually need to return a set of all the hidden trees. Instead, I could have used the same method to count all the trees that are visible. But I decided to return the entire set of hidden trees, just in case we need them later. Turns out we didn’t!!

Finally, we solve the problem:

    grid = Grid(rows)
    print(grid)
    
    # Part 1 - How many visible trees?
    hidden_trees = grid.get_hidden_trees()
    print("Part 1:")
    print(f"Number of hidden trees={len(hidden_trees)}")
    print(f"Number of visible trees={grid.size - len(hidden_trees)}")

Part 2

The elves are satisfied with the area! Now they want to find the best tree for their treehouse. The best tree is the tree with the highest scenic score.

What is the highest scenic score possible for any tree in our grid?

We’re told:

Scenic score is given by product of viewing distance in each of the four directions, i.e. left, right, up, down.
Viewing distance is: how far away is the furthest tree we can see in this direction?
- The viewing distance in any direction is given by: the difference between our location, and the nearest tree that is at least as tall as our tree. I.e. if any tree is as tall as our tree or taller, then we can’t see past it.
- If we’re on an edge looking out, then the viewing distance is 0 in that direction. (And, thus, the scenic score will be 0 for any tree on an edge.)

Here’s my solution…

First, we need to add a couple of methods to our Grid class:

    def get_scenic_scores(self) -> list[int]:
        """ Returns the scenic scores for every tree in the grid """
        scenic_scores = []
        
        # process across then down
        for y in range(self._width):
            for x in range(self._height):
                point = Point(x, y)
                score = self.get_scenic_score_for_point(point)
                scenic_scores.append(score)
        
        return scenic_scores
                
    def get_scenic_score_for_point(self, point: Point) -> int:
        """ Scenic score is given by product of viewing distance in each of the four directions. 
        Viewing distance is given by how far away is the nearest tree that is at least as tall as this one. 
        Viewing distance is always 0 when looking out from an edge. """
        
        this_value = self.height_at_point(point)
        
        # Use generators, since we will just keep getting the next tree
        # until we reach a tree at least as tall. In theory, this is slightly more efficient than lists.
        left = (x for x in reversed(self.rows[point.y][0:point.x]))
        right = (x for x in self.rows[point.y][point.x+1:])
        up = (y for y in reversed(self.cols[point.x][0:point.y]))
        down = (y for y in self.cols[point.x][point.y+1:])
        
        viewing_distances = [] # store our four distances
        for direction in (left, right, up, down):
            distance = 0    # if we're on the edge, this will be the final score.
            for value in direction:
                if value < this_value:
                    distance += 1
                else: # this tree is at least as tall as our tree. We can't see past it.
                    distance += 1 # This is the last tree we can see
                    break # exit inner for

            viewing_distances.append(distance)
        
        return math.prod(viewing_distances)

The get_scenic_score_for_point() method:
- Creates generators to return all the trees in each direction, i.e. left, right, up and down.
  - I’ve used generators, since we don’t need the whole list in each case. We can stop once we’ve found a tree that is at least as tall as our tree. In theory, this will perform a little better.
  - Note that I’ve reversed the left and up directions, since we always want to step away from our tree, one at a time. If we’re going left, that means subtracting one from the x value with each step; and if we’re going up, that means substracting one from the y value with each step.
We then iterate through each direction one at a time, i.e. left, right, up, down.
- Initialise the viewing distance to 0. (It will stay 0 if we’re looking out from an edge.)
- Return the next tree from generator. If it is shorter than our tree, increment our viewing distance.
- If it is as tall or taller, increment our viewing distance and exit the loop. I.e. we can’t see past this tree.
- Finally, return the product of our four viewing distances.
The get_scenic_scores() method calls our get_scenic_score_for_point() method for each tree in the grid. It stores each score in a list, and returns the list.

Finally, we solve like this:

    # Part 2 - What is the maximum scenic score?
    print("\nPart 2:")
    scenic_scores = grid.get_scenic_scores()
    print(f"Highest score={max(scenic_scores)}")

Simples!!

Results

The final code looks like this:

from dataclasses import dataclass
import math
from pathlib import Path
import time

SCRIPT_DIR = Path(__file__).parent
# INPUT_FILE = Path(SCRIPT_DIR, "input/sample_input.txt")
INPUT_FILE = Path(SCRIPT_DIR, "input/input.txt")

@dataclass(frozen=True)
class Point():
    """ Point class """
    x: int
    y: int

class Grid():
    """ Represents a grid of trees heights """
    
    def __init__(self, grid_rows: list) -> None:
        """ Expects data in the format... [[3, 0, 3, 7, 3], [2, 5, 5, 1, 2], ...] """
        self.rows: list[list[int]] = grid_rows
        self.cols = list(zip(*self.rows))
        self._width = len(self.cols)
        self._height = len(self.rows)
        self.size = self._width * self._height
    
    def height_at_point(self, point: Point) -> int:
        return self.rows[point.y][point.x]

    def is_visible(self, point: Point) -> bool:
        """ A tree is visible if it is on any edge, 
        or if there are no taller trees in the same row or column. """
        
        # check if it's on an edge
        if point.x == 0 or point.x == self._width-1:
            return True
        if point.y == 0 or point.y == self._height-1:
            return True
        
        value = self.height_at_point(point)
        # Check if taller than any other tree in the row. If so, it is visible.
        if value > max(self.rows[point.y][0:point.x]): return True
        if value > max(self.rows[point.y][point.x+1:]): return True
        
        # Now check the column. 
        if value > max(self.cols[point.x][0:point.y]): return True
        if value > max(self.cols[point.x][point.y+1:]): return True
        
        return False
    
    def get_hidden_trees(self) -> set[Point]:
        """ Returns all locations where trees are hidden from view. """
        return {Point(x, y) for x in range(self._height)
                            for y in range(self._width)
                            if not self.is_visible(Point(x,y))}
    
    def get_scenic_scores(self) -> list[int]:
        """ Returns the scenic scores for every tree in the grid """
        scenic_scores = []
        
        # process across then down
        for y in range(self._width):
            for x in range(self._height):
                point = Point(x, y)
                score = self.get_scenic_score_for_point(point)
                scenic_scores.append(score)
        
        return scenic_scores
                
    def get_scenic_score_for_point(self, point: Point) -> int:
        """ Scenic score is given by product of viewing distance in each of the four directions. 
        Viewing distance is given by how far away is the nearest tree that is at least as tall as this one. 
        Viewing distance is always 0 when looking out from an edge. """
        
        this_value = self.height_at_point(point)
        
        # Use generators, since we will just keep getting the next tree
        # until we reach a tree at least as tall. In theory, this is slightly more efficient than lists.
        left = (x for x in reversed(self.rows[point.y][0:point.x]))
        right = (x for x in self.rows[point.y][point.x+1:])
        up = (y for y in reversed(self.cols[point.x][0:point.y]))
        down = (y for y in self.cols[point.x][point.y+1:])
        
        viewing_distances = [] # store our four distances
        for direction in (left, right, up, down):
            distance = 0    # if we're on the edge, this will be the final score.
            for value in direction:
                if value < this_value:
                    distance += 1
                else: # this tree is at least as tall as our tree. We can't see past it.
                    distance += 1 # This is the last tree we can see
                    break # exit inner for

            viewing_distances.append(distance)
        
        return math.prod(viewing_distances)
            
    def __repr__(self):
        return (f"{self.__class__.__name__}" 
               + f"(size={self.size}, rows={len(self.rows)}, cols={len(self.cols)})")

def main():
    with open(INPUT_FILE, mode="rt") as f:
        data = f.read().splitlines()
        
    rows = [[int(x) for x in row] for row in data]
    grid = Grid(rows)
    print(grid)
    
    # Part 1 - How many visible trees?
    hidden_trees = grid.get_hidden_trees()
    print("Part 1:")
    print(f"Number of hidden trees={len(hidden_trees)}")
    print(f"Number of visible trees={grid.size - len(hidden_trees)}")
    
    # Part 2 - What is the maximum scenic score?
    print("\nPart 2:")
    scenic_scores = grid.get_scenic_scores()
    print(f"Highest score={max(scenic_scores)}")
    
if __name__ == "__main__":
    t1 = time.perf_counter()
    main()
    t2 = time.perf_counter()
    print(f"Execution time: {t2 - t1:0.4f} seconds")

The output looks like this:

Part 1:
Number of hidden trees=7981
Number of visible trees=1820

Part 2:
Highest score=385112
Execution time: 0.0712 seconds

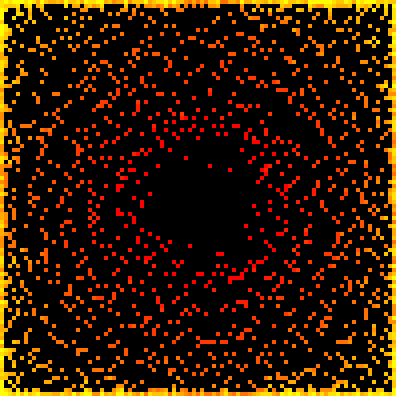
Visualisation

Just for fun, let’s render our tree grid as an image. This is pretty easy to do with the Python Imagining Library (PIL). First we need to install Pillow.

py -m pip install Pillow

Here are the code changes…

First:

Import from PIL.
Store a boolean that turns on or off the image rendering, as required.
Decide where we want to put the generated image file.

from PIL import Image

RENDER = True
OUTPUT_FILE = Path(SCRIPT_DIR, "output/output.png")

Next we’ll add a render_iamge() method to our Grid class:

    def render_image(self, target_width:int=600) -> Image.Image:
        """ Render grid as a heatmap image

        Args:
            width (int, optional): Target width, in pxiels. Defaults to 600.
        """
        scale = target_width // self._width  # our original image is only a few pixels across. We need to scale up.
        
        hidden_trees = self.get_hidden_trees()
        
        # Flatten our x,y array into a single list of height values
        # If the tree is a hidden tree, set its height to -1 in the flattened array
        height_values = [self.height_at_point(Point(x,y)) 
                         if Point(x,y) not in hidden_trees else -1
                                        for y in range(self._height) 
                                        for x in range(self._width)]
        
        max_height = max(height_values)

        # create a new list of RGB values, where each is given by an (R,G,B) tuple.
        # To achieve a yellow->amber->red effect, we want R to always be 255, B to always be 0, and G to vary based on height
        pixel_colour_map = list(map(
                    lambda x: (255, int(255*((max_height-x)/max_height)), 0) if x >= 0 else (0, 0, 0), 
                    height_values))        

        image = Image.new(mode='RGB', size=(self._width, self._height))
        image.putdata(pixel_colour_map)  # load our colour map into the image

        # scale the image and return it
        return image.resize((self._width*scale, self._height*scale), Image.Resampling.NEAREST)

This is how it works:

Take our 2D grid, and convert it to a single flattened list of int values, which are the heights at each location. I.e. all the values from the first row, then all the values from the second row, and so on.
- We’re using a list comprehension to do this.
- Note that our comprehension returns the height if the tree is visible, but otherwise returns -1. This is how we’ll identify hidden trees later.
Create an RGB pixel map, by convert each single height value (which is always going to be in the range 0-9) to an RGB tuple.
- If the tree is not hidden, then our tuple is (255, x, 0) where the value of x is dependent on the height.
- If the tree is hidden, we set our tuple to (0, 0, 0), i.e. black.
Create a new PIL Image object, by loading in our pixel map.
Finally, resize the pixel map to something big enough to see!

Lastly, we just need to save the Image as a file. If the parent directory of the file doesn’t exist, then create it:

    if RENDER:
        dir_path = Path(OUTPUT_FILE).parent
        if not Path.exists(dir_path):
            Path.mkdir(dir_path)

        image = grid.render_image(400)
        image.save(OUTPUT_FILE)

With my actual data, the output looks like this:

Hidden Trees

‹›

Learning Python with Advent of Code Walkthroughs