Learning Python with Advent of Code Walkthroughs
Dazbo's Advent of Code solutions, written in Python
Advent of Code 2022 - Day 23
Useful Links
Concepts and Packages Demonstrated
Enum typedequedefaultdictsetsdisjointMatplotlib
Page Navigation
Problem Intro
Phew. This one was significantly less traumatic than yesterday!!
We need to plant seedlings in a grove. We’re given a map that shows elf positions (marked #) and empty ground (marked .) We need to direct elves to the appropriate positions.
The input data looks something like this:
....#..
..###.#
#...#.#
.#...##
#.###..
##.#.##
.#..#..
Rounds: elves alternative between considering where to move to, and actually moving. The rules are:
- Consideration step:
- Consider all 8 adjacent positions for each elf.
- If no elves in those positions, do nothing in this round.
- Otherwise, propose moving the elf a step in the first valid direction, from a list of directions.
- If there’s more than one elf proposed to a position, none of these elves move.
- Move step: move the elves to their proposed locatiosn.
- Finally, rotate the list of directions (and associated rules).
Part 1
Simulate the Elves’ process and find the smallest rectangle that contains the Elves after 10 rounds. How many empty ground tiles does that rectangle contain?
Here’s my strategy:
- Create a
Pointclass for our(x,y)positions. ThisPointclass knows how to:- Add vectors to create new points.
- We’ll use this to obtain the
setof ALL adjacent points (neighbours) for each location. - And we’ll add another utility method which will only return the adjacent points from a list of directions supplied.
- Create an Enum class to store our 8 vectors, i.e. N, NE, E, SE, etc. This allows us to store all the vectors as a collection of related constants.
@dataclass(frozen=True)
class Point():
""" Point x,y which knows how to add another point,
and how to return all adjacent points, including diagonals. """
x: int
y: int
def all_neighbours(self) -> set[Point]:
""" Return all adjacent orthogonal (not diagonal) Points """
return {(self + vector.value) for vector in list(Vector)}
def get_neighbours(self, directions: list[Vector]) -> set[Point]:
return {(self + vector.value) for vector in list(directions)}
def __add__(self, other) -> Point:
""" Subtract other point from this point, returning new point vector """
return Point(self.x + other.x, self.y + other.y)
def __repr__(self):
return f"P({self.x},{self.y})"
class Vector(Enum):
""" Enumeration of 8 directions, and a rotating list of direction choices. """
N = Point(0, -1)
NE = Point(1, -1)
E = Point(1, 0)
SE = Point(1, 1)
S = Point(0, 1)
SW = Point(-1, 1)
W = Point(-1, 0)
NW = Point(-1, -1)
Now create a Grid class, which is created from the grid of initial elf positions:
class Grid():
""" Stores a set of all elf positions. """
def __init__(self, grid: list[str]) -> None:
self._grid = grid
self._elves: set[Point] = set()
self._initialise_elves()
self._directions = deque([ # use a deque so we can rotate
([Vector.N, Vector.NE, Vector.NW], Vector.N),
([Vector.S, Vector.SE, Vector.SW], Vector.S),
([Vector.W, Vector.NW, Vector.SW], Vector.W),
([Vector.E, Vector.NE, Vector.SE], Vector.E)
])
def _initialise_elves(self):
""" From input, store all current elves - marked with '#' - as a set.
Then define the bounds. """
for y, row in enumerate(self._grid):
for x, val in enumerate(row):
if val == "#":
self._elves.add(Point(x, y))
self._set_bounds()
def _set_bounds(self):
self._min_x = min(point.x for point in self._elves)
self._max_x = max(point.x for point in self._elves)
self._min_y = min(point.y for point in self._elves)
self._max_y = max(point.y for point in self._elves)
def iterate(self) -> int:
""" Perform a single iteration by following the rules.
Returns: the number of elves that moved. """
proposals: dict = {} # E.g. {elf point: proposed point}
for elf_locn in self._elves: # for every existing elf location
# check if this elf has any immediate neighbours
if elf_locn.all_neighbours().isdisjoint(self._elves):
proposals[elf_locn] = None
continue # no neighbours are elves; this elf does nothing
for direction_checks, proposed_direction in self._directions:
if elf_locn.get_neighbours(direction_checks).isdisjoint(self._elves):
proposals[elf_locn] = elf_locn + proposed_direction.value
break # exit at the first matching direction
# turn into {proposed locn: [elf1_locn, elf2_locn, ...], ...}
elves_per_proposal = defaultdict(list)
for elf_locn, proposal in proposals.items():
if proposal is not None:
elves_per_proposal[proposal] += [elf_locn]
# Only move elves that have made a unique proposal
for add, rem in elves_per_proposal.items():
if len(rem) == 1:
self._elves.add(add)
self._elves.remove(rem[0])
self._rotate_direction()
self._set_bounds()
return len(elves_per_proposal)
def _rotate_direction(self):
""" Rotate our directions. I.e. direction n+1 becomes direction n, etc. """
self._directions.rotate(-1)
def score(self) -> int:
""" Count empty squares within the bounds """
total_tiles = (self._max_x+1-self._min_x) * (self._max_y+1 - self._min_y)
elf_count = len(self._elves)
return total_tiles - elf_count
def __str__(self) -> str:
lines = []
for y in range(self._min_y, self._max_y+1):
line = ""
for x in range (self._min_x, self._max_x+1):
line += "#" if Point(x,y) in self._elves else "."
lines.append(line)
return "\n".join(lines)
def __repr__(self) -> str:
return f"Grid(score={self.score})"
Here’s what it does:
- Stores elf positions as a
set, and initialise the bounds, i.e. the minimum and maximumxandyvalues of all our elves. - Stores our
_directionsas a deque, where each member is atupleof:- The
listof three adjacent locations we need to check - The direction the elf should move, if there are no elves in that
list.
- The
- Provides a method to rotate this
deque, i.e. so that the next direction is the new first choice. (And the previous preferred choice is now the last preferred choice.) - Provides a
score()method, which returns the number of empty tiles within the bounds. It does this by calculating the area of the bound rectangle (using the bounds we calculated earlier), and then subtracting the count of all the elves in our set. The difference is the number of empty locations in the ever-expanding rectangle. - The
iterate()method does all the hard work.- Create an empty
dictto store a proposed elf location for each current elf. - For each elf, get all its neighbours. Check if the
setof neighbours is a disjoint with thesetof all existing elf locations. Recall thatisdisjoint()only returnsTrueif there is no overlap between the two sets. If this is the case, then this elf will not move. - Next, iterate through the
_directionsdequein order.- Check each of the three adjacent locations in the current direction check, and if there are no elves in any of those locations, propose the specified new direction.
- Now we need to check if there are any proposed locations that are common to more than one elf.
To do this:
- Create a defaultdict(list) called
elves_per_proposal, that stores alistof current elf locations as the value, and the proposed location as the key. Because this isdefaultdict(list), it will create an empty list for every location key it sees for the first time. - And then, for every elf that is proposed to this location, we simply add the current elf.
- Then, we iterate over this
defaultdicrt, and wherever thelistvalue has exactly one member, we know that this target location has been uniquely proposed. In which case, remove the current position from_elvesand add the new proposed position to_elves. - Wherever the list length is not
1, we do nothing.
- Create a defaultdict(list) called
- From here, create dict of {candidate locn: [elf1, elf2, …]}
- Finally, the method returns the number of elves that moved. (We’ll use this in Part 2.)
- Create an empty
Now we can solve Part 1 by calling our grid.iterate() 10 times:
def main():
with open(INPUT_FILE, mode="rt") as f:
data = f.read().splitlines()
grid = Grid(data)
# Part 1
current_round = 1
for _ in range(10):
grid.iterate()
current_round += 1
print(f"Part 1: score={grid.score()}")
Part 2
Figure out where the Elves need to go. What is the number of the first round where no Elf moves?
Now we simply need to iterate until the elves don’t move any more. This is trivial to achieve, since our iterate() method already returns the count of the number of elves that moved in the last iteration. So we just need to iterate until this returns 0.
while grid.iterate() > 0:
current_round += 1
print(f"Part 2: Stable at round {current_round}")
Results
Here’s the final code:
from __future__ import annotations
from collections import deque, defaultdict
from dataclasses import dataclass
from enum import Enum
from pathlib import Path
import time
SCRIPT_DIR = Path(__file__).parent
# INPUT_FILE = Path(SCRIPT_DIR, "input/sample_input.txt")
INPUT_FILE = Path(SCRIPT_DIR, "input/input.txt")
@dataclass(frozen=True)
class Point():
""" Point x,y which knows how to add another point,
and how to return all adjacent points, including diagonals. """
x: int
y: int
def all_neighbours(self) -> set[Point]:
""" Return all adjacent orthogonal (not diagonal) Points """
return {(self + vector.value) for vector in list(Vector)}
def get_neighbours(self, directions: list[Vector]) -> set[Point]:
return {(self + vector.value) for vector in list(directions)}
def __add__(self, other) -> Point:
""" Subtract other point from this point, returning new point vector """
return Point(self.x + other.x, self.y + other.y)
def __repr__(self):
return f"P({self.x},{self.y})"
class Vector(Enum):
""" Enumeration of 8 directions, and a rotating list of direction choices. """
N = Point(0, -1)
NE = Point(1, -1)
E = Point(1, 0)
SE = Point(1, 1)
S = Point(0, 1)
SW = Point(-1, 1)
W = Point(-1, 0)
NW = Point(-1, -1)
class Grid():
""" Stores a set of all elf positions. """
def __init__(self, grid: list[str]) -> None:
self._grid = grid
self._elves: set[Point] = set()
self._initialise_elves()
self._directions = deque([ # use a deque so we can rotate
([Vector.N, Vector.NE, Vector.NW], Vector.N),
([Vector.S, Vector.SE, Vector.SW], Vector.S),
([Vector.W, Vector.NW, Vector.SW], Vector.W),
([Vector.E, Vector.NE, Vector.SE], Vector.E)
])
def _initialise_elves(self):
""" From input, store all current elves - marked with '#' - as a set.
Then define the bounds. """
for y, row in enumerate(self._grid):
for x, val in enumerate(row):
if val == "#":
self._elves.add(Point(x, y))
self._set_bounds()
def _set_bounds(self):
self._min_x = min(point.x for point in self._elves)
self._max_x = max(point.x for point in self._elves)
self._min_y = min(point.y for point in self._elves)
self._max_y = max(point.y for point in self._elves)
def iterate(self) -> int:
""" Perform a single iteration by following the rules.
Returns: the number of elves that moved. """
proposals: dict = {} # E.g. {elf point: proposed point}
for elf_locn in self._elves: # for every existing elf location
# check if this elf has any immediate neighbours
if elf_locn.all_neighbours().isdisjoint(self._elves):
proposals[elf_locn] = None
continue # no neighbours are elves; this elf does nothing
for direction_checks, proposed_direction in self._directions:
if elf_locn.get_neighbours(direction_checks).isdisjoint(self._elves):
proposals[elf_locn] = elf_locn + proposed_direction.value
break # exit at the first matching direction
# turn into {proposed locn: [elf1_locn, elf2_locn, ...], ...}
elves_per_proposal = defaultdict(list)
for elf_locn, proposal in proposals.items():
if proposal is not None:
elves_per_proposal[proposal] += [elf_locn]
# Only move elves that have made a unique proposal
for add, rem in elves_per_proposal.items():
if len(rem) == 1:
self._elves.add(add)
self._elves.remove(rem[0])
self._rotate_direction()
self._set_bounds()
return len(elves_per_proposal)
def _rotate_direction(self):
""" Rotate our directions. I.e. direction n+1 becomes direction n, etc. """
self._directions.rotate(-1)
def score(self) -> int:
""" Count empty squares within the bounds """
total_tiles = (self._max_x+1-self._min_x) * (self._max_y+1 - self._min_y)
elf_count = len(self._elves)
return total_tiles - elf_count
def __str__(self) -> str:
lines = []
for y in range(self._min_y, self._max_y+1):
line = ""
for x in range (self._min_x, self._max_x+1):
line += "#" if Point(x,y) in self._elves else "."
lines.append(line)
return "\n".join(lines)
def __repr__(self) -> str:
return f"Grid(score={self.score})"
def main():
with open(INPUT_FILE, mode="rt") as f:
data = f.read().splitlines()
grid = Grid(data)
print(f"{grid}\n")
# Part 1
current_round = 1
for _ in range(10):
grid.iterate()
current_round += 1
print(f"Part 1: score={grid.score()}")
while grid.iterate() > 0:
current_round += 1
print(f"Part 2: Stable at round {current_round}")
if __name__ == "__main__":
t1 = time.perf_counter()
main()
t2 = time.perf_counter()
print(f"Execution time: {t2 - t1:0.4f} seconds")
Here’s the output:
Part 1: score=4181
Part 2: Stable at round 973
Execution time: 31.3521 seconds
It could be a bit quicker, I guess! Maybe I’ll optimise it sometime.
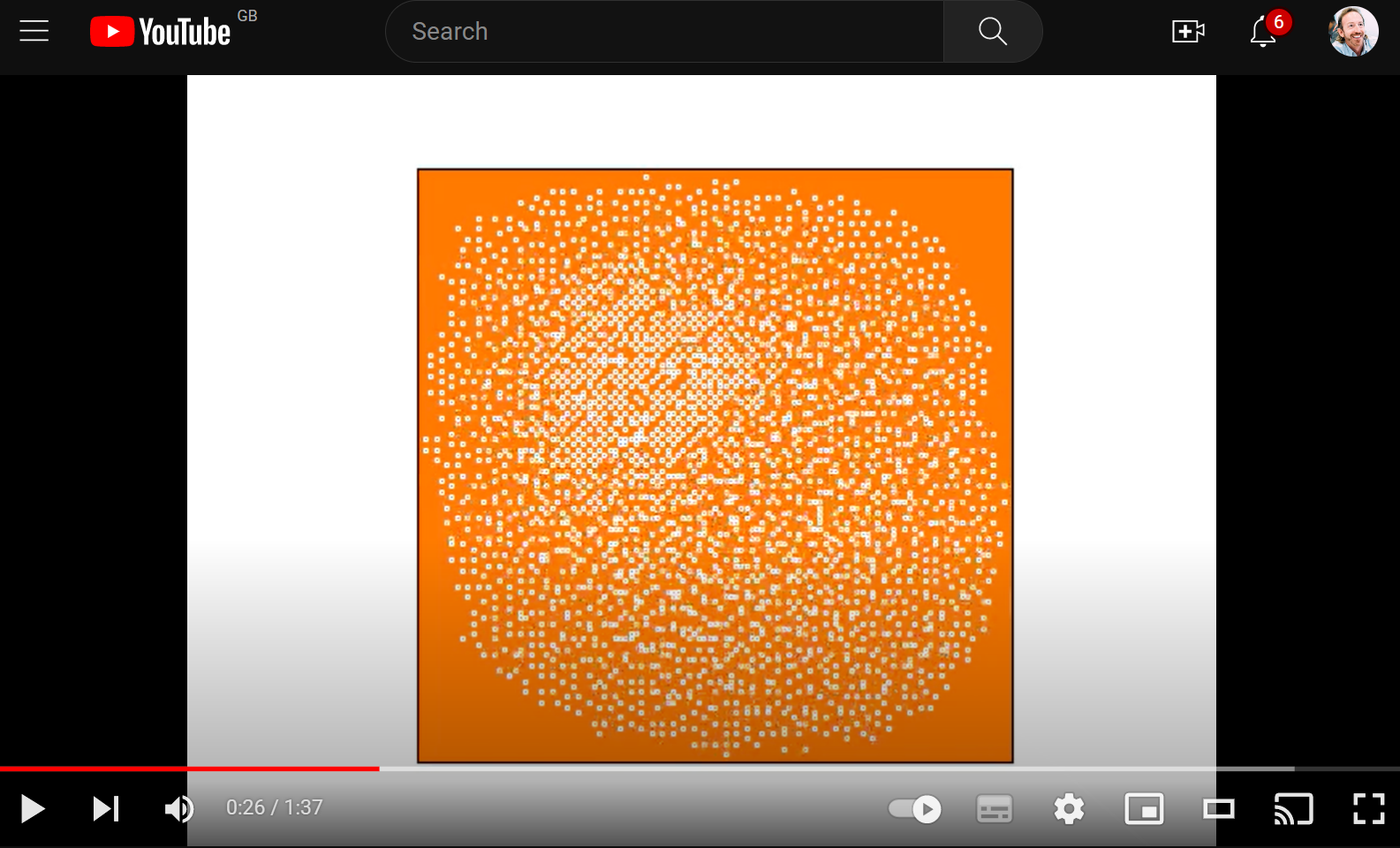
Visualisation
I thought it would be cool to add a vis. I’ve done that using my usual Animator class.
Here’s the updated code…
from __future__ import annotations
from collections import deque, defaultdict
from dataclasses import dataclass
from enum import Enum
from io import BytesIO
from pathlib import Path
import time
import imageio as iio
from matplotlib import pyplot as plt
from matplotlib.markers import MarkerStyle
from tqdm import tqdm
SCRIPT_DIR = Path(__file__).parent
# INPUT_FILE = Path(SCRIPT_DIR, "input/sample_input.txt")
INPUT_FILE = Path(SCRIPT_DIR, "input/input.txt")
ENABLE_ANIMATIONS = True
OUTPUT_FOLDER = Path(SCRIPT_DIR, "output/")
@dataclass(frozen=True)
class Point():
""" Point x,y which knows how to add another point,
and how to return all adjacent points, including diagonals. """
x: int
y: int
def all_neighbours(self) -> set[Point]:
""" Return all adjacent orthogonal (not diagonal) Points """
return {(self + vector.value) for vector in list(Vector)}
def get_neighbours(self, directions: list[Vector]) -> set[Point]:
return {(self + vector.value) for vector in list(directions)}
def __add__(self, other) -> Point:
""" Subtract other point from this point, returning new point vector """
return Point(self.x + other.x, self.y + other.y)
def __repr__(self):
return f"P({self.x},{self.y})"
class Vector(Enum):
""" Enumeration of 8 directions, and a rotating list of direction choices. """
N = Point(0, -1)
NE = Point(1, -1)
E = Point(1, 0)
SE = Point(1, 1)
S = Point(0, 1)
SW = Point(-1, 1)
W = Point(-1, 0)
NW = Point(-1, -1)
class Animator():
""" Creates an animation file of specified target size.
Designed to be used as Context Manager. E.g.
with Animator(file=Path("path/to/file""), fps=num) as animator:
# code
"""
def __enter__(self):
""" Required for ContextManager implementation. """
if self._enabled:
self._create_path()
return self # so the as <name> returns an object
def __exit__(self, exc_type, exc_val, exc_tb):
""" Required for ContextManager implementation. """
if self._enabled:
self._save_anim()
def __init__(self, file: Path, fps: int, loop=1, enabled=True) -> None:
""" Create an Animator. Suggest the file should be a .gif.
Set frames per second (fps).
Set loop to 0, to loop indefinitely. Default is 1. """
self._enabled = enabled
self._outputfile = file
self._frames = [] # can be in-memory BytesIO objects, or files
self._fps = fps
self._loop = loop
@property
def enabled(self):
return self._enabled
@enabled.setter
def enabled(self, value: bool):
self._enabled = value
def _create_path(self):
if self._enabled:
dir_path = Path(self._outputfile).parent
if not Path.exists(dir_path):
Path.mkdir(dir_path)
def _save_anim(self):
""" Takes animation frames, and converts to a single animated file. """
with iio.get_writer(self._outputfile, mode='I', fps=self._fps, loop=self._loop) as writer:
for frame in tqdm(self._frames):
image = iio.v3.imread(frame)
writer.append_data(image)
print(f"Animation saved to {self._outputfile}")
def add_frame(self, frame):
""" Add a frame to the animation.
The frame can be in the form of a BytesIO object, or a file Path
"""
self._frames.append(frame)
class Grid():
""" Stores a set of all elf positions. """
def __init__(self, grid: list[str], animator=None) -> None:
self._grid = grid
self._elves: set[Point] = set()
self._animator: Animator = animator
self._initialise_elves()
self._directions = deque([ # use a deque so we can rotate
([Vector.N, Vector.NE, Vector.NW], Vector.N),
([Vector.S, Vector.SE, Vector.SW], Vector.S),
([Vector.W, Vector.NW, Vector.SW], Vector.W),
([Vector.E, Vector.NE, Vector.SE], Vector.E)
])
self.plt_data = self.init_plot()
def _initialise_elves(self):
""" From input, store all current elves - marked with '#' - as a set.
Then define the bounds. """
for y, row in enumerate(self._grid):
for x, val in enumerate(row):
if val == "#":
self._elves.add(Point(x, y))
self._set_bounds()
def _set_bounds(self):
self._min_x = min(point.x for point in self._elves)
self._max_x = max(point.x for point in self._elves)
self._min_y = min(point.y for point in self._elves)
self._max_y = max(point.y for point in self._elves)
def iterate(self) -> int:
""" Perform a single iteration by following the rules.
Returns: the number of elves that moved. """
proposals: dict = {} # E.g. {elf point: proposed point}
for elf_locn in self._elves: # for every existing elf location
# check if this elf has any immediate neighbours
if elf_locn.all_neighbours().isdisjoint(self._elves):
proposals[elf_locn] = None
continue # no neighbours are elves; this elf does nothing
for direction_checks, proposed_direction in self._directions:
if elf_locn.get_neighbours(direction_checks).isdisjoint(self._elves):
proposals[elf_locn] = elf_locn + proposed_direction.value
break # exit at the first matching direction
# turn into {proposed locn: [elf1_locn, elf2_locn, ...], ...}
elves_per_proposal = defaultdict(list)
for elf_locn, proposal in proposals.items():
if proposal is not None:
elves_per_proposal[proposal] += [elf_locn]
# Only move elves that have made a unique proposal
for add, rem in elves_per_proposal.items():
if len(rem) == 1:
self._elves.add(add)
self._elves.remove(rem[0])
self._rotate_direction()
self._set_bounds()
if self._animator and self._animator.enabled:
self.vis_state()
return len(elves_per_proposal)
def _rotate_direction(self):
""" Rotate our directions. I.e. direction n+1 becomes direction n, etc. """
self._directions.rotate(-1)
def score(self) -> int:
""" Count empty squares within the bounds """
total_tiles = (self._max_x+1-self._min_x) * (self._max_y+1 - self._min_y)
elf_count = len(self._elves)
return total_tiles - elf_count
def __str__(self) -> str:
lines = []
for y in range(self._min_y, self._max_y+1):
line = ""
for x in range (self._min_x, self._max_x+1):
line += "#" if Point(x,y) in self._elves else "."
lines.append(line)
return "\n".join(lines)
def __repr__(self) -> str:
return f"Grid(score={self.score})"
def init_plot(self) -> tuple:
fig, axes = plt.subplots()
axes.get_xaxis().set_visible(False)
axes.get_yaxis().set_visible(False)
axes.set_facecolor('xkcd:orange')
return fig, axes
def vis_state(self):
fig, axes = self.plt_data
axes.clear()
shape = 's'
all_x, all_y = zip(*((point.x+0.5, point.y+0.5) for point in self._elves))
axes.set_xlim(self._min_x-1, self._max_x+2)
axes.set_ylim(self._min_y-1, self._max_y+2)
axes.set_aspect("equal")
axes.invert_yaxis()
# dynamically compute the marker size
fig.canvas.draw()
sz = ((axes.get_window_extent().width / (self._max_x-self._min_x) * (48/fig.dpi)) ** 2)
axes.scatter(all_x, all_y, marker=MarkerStyle(shape), s=sz,
color='black', edgecolors='white')
# save the plot as a frame; store the frame in-memory, using a BytesIO buffer
frame = BytesIO()
plt.savefig(frame, format='png') # save to memory, rather than file
self._animator.add_frame(frame)
# plt.show()
def main():
with open(INPUT_FILE, mode="rt") as f:
data = f.read().splitlines()
with Animator(file=Path(OUTPUT_FOLDER, "grid_anim.gif"), fps=10, enabled=ENABLE_ANIMATIONS) as animator:
# Part 1
grid = Grid(data, animator=animator)
current_round = 1
for _ in range(10):
grid.iterate()
current_round += 1
print(f"Part 1: score={grid.score()}")
# Part 2
print(f"{grid}\n")
while grid.iterate() > 0:
current_round += 1
print(f"Part 2: Stable at round {current_round}")
if __name__ == "__main__":
t1 = time.perf_counter()
main()
t2 = time.perf_counter()
print(f"Execution time: {t2 - t1:0.4f} seconds")