Learning Python with Advent of Code Walkthroughs
Dazbo's Advent of Code solutions, written in Python

Advent of Code 2022 - Day 22
Useful Links
Concepts and Packages Demonstrated
EnumComprehensionClassDataclassClass InheritanceLiteral_Eval
Page Navigation
Problem Intro
Part 1 was okay. Part 2 was horrendous.
We’re given a strange map and told we have to navigate it by following a specific path. The map is composed of locations, which can be empty or tiles.
- Tiles are valid locations on the map.
- Tiles can be
., which means this tile can be occoupied. - Alternatively, tiles can be
#, meaning that this tile is blocked.
- Tiles can be
- Empty locations are represented by ` `, and these are NOT valid locations to visit.
Our input data is composed of two components:
- The map we must navigate.
- A sequence of alternating numbers and letters:
Number means: move forward
ntiles; stop if you hit an obstacle. Letter means: turn left (L) or right (R), at current position. I.e. rotate left or right, relative to your current orientation.
Here is some sample input data:
...#
.#..
#...
....
...#.......#
........#...
..#....#....
..........#.
...#....
.....#..
.#......
......#.
10R5L5R10L4R5L5
We’re told that if we go off the map (well, more accurately, off the tiles), then we reappear at the tile on the opposite side. (Assuming not blocked.)
The final password is the sum of 1000 times the row, 4 times the column, and the last facing. Note that rows and columns are 1-indexed. Facing values:
- 0 for right (>)
- 1 for down (v)
- 2 for left (<)
- 3 for up (^).
Part 1
What is the final password?
Part 1 is easy enough. We need to:
- Split the input data into the its two components: the map and the instructions.
- We need a method to move us forward by a specified number of tiles.
- But we stop if we reach a
#. - And we wrap around to the opposite side if we reach the edge of the map, or an empty space.
- But we stop if we reach a
- We need a method to rotate us left or right, by 90 degrees.
First, I create a Point class, as I often do!
@dataclass(frozen=True)
class Point():
""" Point class, which knows how to return a list of all adjacent coordinates """
x: int
y: int
def __add__(self, other):
""" Subtract other point from this point, returning new point vector """
return Point(self.x + other.x, self.y + other.y)
def neighbours(self) -> list[Point]:
""" Return all adjacent orthogonal (not diagonal) Points """
return [Point(self.x+dx, self.y+dy) for dx in range(-1, 2)
for dy in range(-1, 2)
if abs(dy) != abs(dx)]
def __str__(self):
return f"P({self.x}, {self.y})"
There’s nothing new to say about this. As I often do, this Point class knows how to find the Points that make up its adjacent neighbours.
Now I read in the input data:
def main():
with open(INPUT_FILE, mode="rt") as f:
map_data, instructions = f.read().split("\n\n") # input is two blocks, separated by a line
map_data = map_data.splitlines()
Now some vector stuff:
DIRECTION_SYMBOLS = ['>', 'v', '<', '^'] # Orientation vector key
VECTOR_COORDS = [(1, 0), (0, 1), (-1, 0), (0, -1)]
VECTORS = [Point(*v) for v in VECTOR_COORDS] # so we can retrieve by index
- The
DIRECTION_SYMBOLSis only used for rendering our map visually. - The
VECTOR_COORDSallows us to get our four direction vectors by index. E.g.VECTOR_COORDS[0]gives us a vector of(1, 0). VECTORSis a conveniencelistthat allows us to retrieve any of these vectors inPointform.
Now I’ll create a Map class to do all the hard work:
class Map():
def __init__(self, grid: list[str]) -> None:
self._grid = grid # store original input grid
self._height = len(self._grid)
self._width = max(len(line) for line in self._grid) # the widest line
self._grid = self._pad_grid() # make all rows same length
self._cols = self._generate_cols()
self._staert = Point(0,0)
self._posn = Point(0,0)
self._direction = 0
self._path = {}
self._set_start() # Initialise top-left, pointing right
self._last_instruction = "" # just to help with debugging
def _generate_cols(self):
""" Create a list of str, where each str is a column.
E.g. first col could be ' .... '
"""
cols_list = list(zip(*self._grid))
return ["".join(str(char) for char in col) for col in cols_list]
def _set_start(self):
""" Start position is first open space on the grid,
starting at (0, 0) - which could be in 'emtpy' space, and moving right. """
first_space = self._grid[0].find(".")
self._posn = Point(first_space, 0)
self._start = self._posn
self._direction = 0 # index of ['>', 'v', '<', '^']
self._path = {self._posn: self._direction} # Everywhere we've been, including direction
def _pad_grid(self):
""" Make all rows are the same length. """
return [line + " " * (self._width - len(line)) if len(line) < self._width else line for line in self._grid]
@property
def posn(self) -> Point:
""" Point coordinate of the current position. """
return self._posn
def move(self, instruction: str):
""" Can be direction instruction, i.e. L or R, or a move forward instruction, e.g. 10 """
self._last_instruction = instruction
if instruction.isdigit():
self._move_forward(int(instruction))
else:
self._change_direction(instruction)
def _change_direction(self, instruction):
""" Rotate to the left or the right, relative to current orientation. """
change = 1 if instruction == "R" else 3 # add 3 rather than -1, to avoid negative mod
self._direction = (self._direction+change) % len(VECTORS)
self._path[self._posn] = self._direction # update direction in the path
def _move_forward(self, steps: int):
""" Move in the current direction until we hit an obstacle. """
for _ in range(steps):
candidate = self._next_posn()
if self._is_possible(candidate):
self._posn = candidate
self._path[self._posn] = self._direction # update direction in path
else: # we need to stop here
break
def _get_row_length(self, row_num: int):
return len(self._grid[row_num]) - self._grid[row_num].count(" ")
def _get_col_length(self, col_num: int):
return len(self._cols[col_num]) - self._cols[col_num].count(" ")
def _next_posn(self) -> Point:
""" Determine next Point in this direction, including wrapping. Does not check if blocked. """
next_posn = self._posn + VECTORS[self._direction]
if not self._is_tile(next_posn): # we're off the tiles, so we need to wrap
# Subtract vector in the opposite direction equal to the length of the row / col
new_x = next_posn.x - VECTORS[self._direction].x * self._get_row_length(self._posn.y)
new_y = next_posn.y - VECTORS[self._direction].y * self._get_col_length(self._posn.x)
next_posn = Point(new_x, new_y)
return next_posn
def _is_tile(self, point: Point) -> bool:
""" Check if the specified point is a tile. I.e. within the bounds and not empty. """
if point.y < 0 or point.y >= len(self._grid):
return False
# check not outside the bounds of the current row. (Allow for variable length row)
if point.x < 0 or point.x >= len(self._grid[point.y]):
return False
# If we've got this far, we're within the bounds of the input data, but it could still be empty
if self._get_value(point) == " ":
return False
return True
def _get_value(self, point: Point) -> str:
""" The value of the grid at the specified point. """
return self._grid[point.y][point.x]
def _is_possible(self, locn: Point):
""" Check if this space is open. Only '.' counts as open. """
return True if self._get_value(locn) == "." else False
def score(self) -> int:
""" Score is given by sum of: (1000*y), (4*x), facing.
For this calculation, x and y are 1-indexed. Facing = direction index. """
return 1000*(self.posn.y+1) + 4*(self.posn.x+1) + self._direction
def __str__(self) -> str:
lines = []
for y, row in enumerate(self._grid):
line = ""
for x, val in enumerate(row):
posn = Point(x,y)
if posn == self._posn:
line += (Colours.RED.value + Colours.BOLD.value
+ DIRECTION_SYMBOLS[self._path[posn]] + Colours.RESET.value)
elif posn == self._start:
line += (Colours.YELLOW.value + Colours.BOLD.value
+ DIRECTION_SYMBOLS[self._path[posn]] + Colours.RESET.value)
elif posn in self._path:
line += Colours.CYAN.value + DIRECTION_SYMBOLS[self._path[posn]] + Colours.RESET.value
else:
line += val
lines.append(line)
return "\n".join(lines)
def __repr__(self):
return f"Map(posn={self.posn}, last_instr={self._last_instruction}, score={self.score()})"
Things to say about this:
- The
Mapclass is instantiated by passing in the grid from our input data. - It determines the height and the width of the grid, at its widest points. Note that the input data may be missing trailing spaces on rows that have empty space at the end.
- It pads out any short rows, so that all rows are the same length.
- It stores the start position, and sets it to the current position, i.e.
self._posn. It also stores the current direction (as theintrepresentation. - It stores the path taken, which is a
dictwith key ofPointand value ofdirection. Thus, it is a path made up of every point we’ve visited in the path, along with the direction we were last facing when we were at that point. - The
move()method handles the current instruction, which can be either a number (i.i.e. the number of spaces to move forward), orL/R. - If the instruction is
LorR, we call the_change_direction()method.- If we’re turning right, we need to increment the direction vector by 1. (E.g. since 0 is right, then 1 is down.)
- If we’re turning to the left, we need to decrement the direction vector by 1.
- However, we also want to wrap around, e.g. if we’re at 3, we need the next direction to be 0.
- The easiest way to achieve all the above is to add
1forR, add3forL, and to mod the result with4. - We then store the result as our current
_direction.
- If the instruction is a number, we call the
_move_forward()method.- Here, we call
_next_posn()for each move we need to take. Each move gives us our nextcandidateposition. This method adds one unit of the current direction vector to the current position. If, after adding the vector, we land on a tile, then this new position is viable. If not, then we need to wrap around. To do that, I simply add a vector in the reverse direction, with a magnitude equal to the length of the row / column. - If the new candidate position is allowed (i.e. it is a
.), we update_posn, and we add the position/direction to the_path. - If the candidate position is blocked (
#), then we need to stop here.
- Here, we call
- I’ve included a
score()method, which returns the final password, as required by the problem. - And lastly, I’ve added a
__str__()method which renders the map to the console. Here I’ve added a bit of colour, to make it obvious where we started, and where we finished:
class Colours(Enum):
""" ANSI escape sequences for coloured console output """
RED = "\033[31m"
GREEN = "\033[32m"
YELLOW = "\033[33m"
BLUE = "\033[34m"
MAGENTA = "\033[35m"
CYAN = "\033[36m"
BOLD = "\033[1m"
RESET = "\033[0m"
So now, I’m ready to solve Part 1:
def main():
with open(INPUT_FILE, mode="rt") as f:
map_data, instructions = f.read().split("\n\n") # input is two blocks, separated by a line
map_data = map_data.splitlines()
the_map = Map(map_data)
process_instructions(instructions, the_map)
print(the_map)
print(f"Part 1: score={the_map.score()}")
def process_instructions(instructions, the_map):
next_transition = 0
this_instr = ""
for i, char in enumerate(instructions):
if i < next_transition:
continue
if char.isdigit():
for j, later_char in enumerate(instructions[i:len(instructions)], i):
if not later_char.isdigit():
next_transition = j
this_instr = instructions[i: next_transition]
break
else: # we've reached the end
this_instr = instructions[i]
else: # we're processing alphabetical characters
this_instr = instructions[i]
the_map.move(this_instr)
How I handle in the instructions line is interesting. Basically, I enumerate the line so that each iteration of the outer loop returns a character, along with the index position of that character.
- If the current character is a digit, then this instruction is a number, and the number could have any length. So process subsequent chracters until the character is no longer a digit. This gives us our transition index, i.e. where we transition back to a
Lor aR. Then just grab all the characters between the first digit, and the transition. This gives us the number for our current move. - If the current character is not a digit, then it must be
LorR, and this instruction is only one character long.
After running this for the sample data, this is what I see:
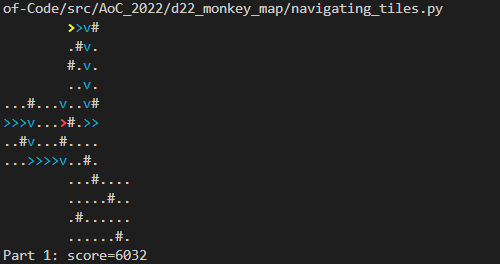
Part 2
Oh dear. The map actually represents an unfolded cube. You can divide the map into 6 square faces. Any part of the map that is empty is not part of the foldable cube. With the sample data, the cube faces can be shown as follows:
1111
1111
1111
1111
222233334444
222233334444
222233334444
222233334444
55556666
55556666
55556666
55556666
Now we’re told that instead of wrapping between left and right, or between top and bottom, if we now get to the edge of any tiles, we need to wrap around as though this were a folded cube. Other than that, the problem is the same.
Fold the map into a cube, then follow the path given in the monkeys’ notes. What is the final password?
For me, the first thing I needed to do was visualise the problem. Here’s my attempt to do this with the sample data:
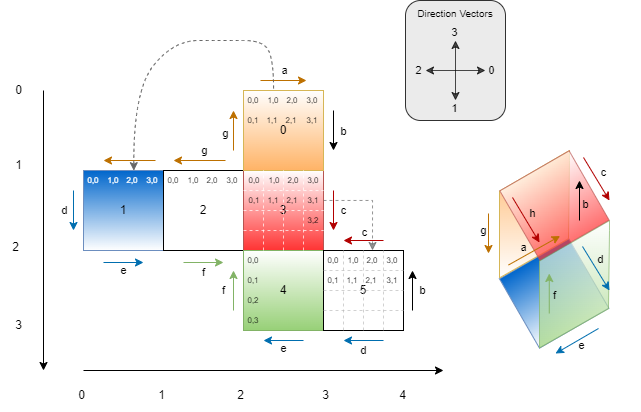
I’ve added a coordinate system, so that we can locate each numbered face by simple coordinates. The coordinates can be expressed as follows:
[(2,0), (0,1), (1,1), (2,1), (2,2), (3,2)] # Faces 0-5
I’ve also added coloured arrows that represent matching edges of folded faces. With this information, we can determine that (for example):
- If I leave the map facing up from face
0, then I’m leaving at edgea. So I’ll reappear on the map in face1, but I’ll be travelling downwards. - Why? Because the
aarrow for face1is at 180 degrees, relative to theaarrow for face0. And consequently, if I was travelling up when I left face0, then I must be now facing down when I enter face1.
Note that these directions only make sense in the 2D representation.
I can build a map of all possible ways of leaving a face, with the corresponding entrance to a different face, like this:
{ # each tuple is (face #, direction)
(0, 3): (1, 1), # arrow a
(0, 2): (2, 1), # arrow g
(0, 0): (5, 2), # arrow b
(1, 3): (0, 1), # arrow a
(1, 2): (5, 3), # arrow d
(1, 1): (4, 3), # arrow e
(2, 3): (0, 0), # arrow g
(2, 1): (4, 0), # arrow f
(3, 0): (5, 1), # arrow c
(4, 2): (2, 3), # arrow f
(4, 1): (1, 3), # arrow e
(5, 3): (3, 2), # arrow c
(5, 0): (0, 2), # arrow b
(5, 1): (1, 0) # arrow d
}
So in the map above, we can see that (0,3) maps to (1,1). What this means is: if you leave face 0 with direction 3 (i.e. up), then you’ll enter face 1 with direction 1 (i.e. down).
To solve for Part 2, here’s my strategy:
- First, externalise this cube’s geometry into a separate input file. This is because the real data uses a different cube geometry. So I’ve got different files to represent my two cubes. The input file for the sample data cube looks like this:
# 0
# 123
# 45
[
[(2,0), (0,1), (1,1), (2,1), (2,2), (3,2)], # Faces 0-5
{ # each tuple is (face #, direction)
(0, 3): (1, 1), # arrow a
(0, 2): (2, 1), # arrow g
(0, 0): (5, 2), # arrow b
(1, 3): (0, 1), # arrow a
(1, 2): (5, 3), # arrow d
(1, 1): (4, 3), # arrow e
(2, 3): (0, 0), # arrow g
(2, 1): (4, 0), # arrow f
(3, 0): (5, 1), # arrow c
(4, 2): (2, 3), # arrow f
(4, 1): (1, 3), # arrow e
(5, 3): (3, 2), # arrow c
(5, 0): (0, 2), # arrow b
(5, 1): (1, 0) # arrow d
}
]
Note that I’ve represented the cube data in Python list format. For this reason, I can read in the file as though it were a Python list, using literal_eval():
with open(INPUT_CUBE, mode="rt") as f: # read in Cube input, in Python list format
cube_data = literal_eval(f.read())
Thus, cube_data is now a list, where element 0 is the list of faces, and element 1 is the dict of edge mappings.
Then I create a new CubeMap class that extends Map, and which requires the face_coords and edge mapping data for our specific cube.
- This class will determine the edge length of our faces.
- It overrides the
_next_posn()method, so that when we reach an edge, instead of wrapping top-to-bottom or left-to-right, it:- Determines the face we will be entering, and the direction we will enter from, using the edge map.
- Establishes the current relative
x, ycoordinate within this face. - Determines the new
x, ycoordinate we need when we enter the next face, in terms of a coordinate within that face. - Converts the target face coordinate to a coordinate in the overall 2D grid.
- Returns this new coordinate, along with the new direction.
Nothing else needs to change!!
The code for new class looks like this:
class CubeMap(Map):
""" Take a 2D grid that is made up of 6 regions, and convert to a cube.
The face coordinates of the Cube must be supplied. """
def __init__(self, grid: list[str], face_coords: list[tuple], face_edge_map: dict[tuple, tuple]) -> None:
super().__init__(grid)
self._face_coords = face_coords # the coordinates of the top-left vertices of this cube
self._face_edge_map = face_edge_map
self._h_faces_width = max(x for x,y in self._face_coords) + 1 # e.g. 4 faces wide
self._v_faces_height = max(y for x,y in self._face_coords) + 1 # e.g. 3 faces tall
self._face_width = self._width // self._h_faces_width # E.g. 4, or 50 with real
self._face_height = self._height // self._v_faces_height # E.g. 4 or 50 with real"
assert self._face_width == self._face_height, "Faces should be squares!"
def _origin_face(self) -> int:
""" Get the face number (index) that this point lives in """
face_x = self._posn.x // self._face_width
face_y = self._posn.y // self._face_width
return self._face_coords.index((face_x, face_y))
def _next_posn(self) -> tuple[Point, int]:
""" Determine next Point in this direction, including wrapping. Does not check if blocked. """
next_posn = self._posn + VECTORS[self._direction]
next_dir = self._direction
if not self._is_tile(next_posn):
# we're off the tiles, so we need to wrap around the cube
next_posn, next_dir = self._next_face_point()
return next_posn, next_dir
def _next_face_point(self) -> tuple[Point, int]:
dest_face, dest_direction = self._face_edge_map[(self._origin_face(), self._direction)]
# print(f"Moving to face {dest_face}, with direction={DIRECTION_SYMBOLS[dest_direction]}")
current_face_x = self.posn.x % self._face_width
current_face_y = self.posn.y % self._face_height
other = 0
dest_face_point = Point(0,0)
match self._direction: # which way are we currently going?
case 0: # >
assert current_face_x == self._face_width - 1, "We must be on a right edge"
other = current_face_y
case 1: # v
assert current_face_y == self._face_height - 1, "We must be on a bottom edge"
other = self._face_width - 1 - current_face_x
case 2: # <
assert current_face_x == 0, "We must be on a left edge"
other = self._face_height - 1 - current_face_y
case 3: # ^
assert current_face_y == 0, "We must be on a top edge"
other = current_face_x
match dest_direction: # which way will we be going?
case 0: # >
dest_face_point = Point(0, other)
case 1: # v
dest_face_point = Point(self._face_height - 1 - other, 0)
case 2: # <
dest_face_point = Point(self._face_height - 1, self._face_width - 1 - other)
case 3: # ^
dest_face_point = Point(other, self._face_width - 1)
# convert face point to grid point
return (self._face_point_to_grid_point(dest_face_point, dest_face), dest_direction)
def _face_point_to_grid_point(self, face_point: Point, face: int) -> Point:
return Point(face_point.x + self._face_coords[face][0]*self._face_width,
face_point.y + self._face_coords[face][1]*self._face_height)
Now we’re ready to call it:
cube = CubeMap(map_data, face_coords=cube_data[0], face_edge_map=cube_data[1])
process_instructions(instructions, cube)
print(f"Part 2: score={cube.score()}")
Results
The final code looks like this:
from __future__ import annotations
from ast import literal_eval
from dataclasses import dataclass
from enum import Enum
from pathlib import Path
import time
SCRIPT_DIR = Path(__file__).parent
# INPUT_FILE = Path(SCRIPT_DIR, "input/sample_input.txt")
# INPUT_CUBE = Path(SCRIPT_DIR, "input/sample_cube_in.txt")
INPUT_FILE = Path(SCRIPT_DIR, "input/input.txt")
INPUT_CUBE = Path(SCRIPT_DIR, "input/cube_in.txt")
class Colours(Enum):
""" ANSI escape sequences for coloured console output """
RED = "\033[31m"
GREEN = "\033[32m"
YELLOW = "\033[33m"
BLUE = "\033[34m"
MAGENTA = "\033[35m"
CYAN = "\033[36m"
BOLD = "\033[1m"
RESET = "\033[0m"
@dataclass(frozen=True)
class Point():
""" Point class, which knows how to return a list of all adjacent coordinates """
x: int
y: int
def __add__(self, other):
""" Subtract other point from this point, returning new point vector """
return Point(self.x + other.x, self.y + other.y)
def neighbours(self) -> list[Point]:
""" Return all adjacent orthogonal (not diagonal) Points """
return [Point(self.x+dx, self.y+dy) for dx in range(-1, 2)
for dy in range(-1, 2)
if abs(dy) != abs(dx)]
def __str__(self):
return f"P({self.x}, {self.y})"
DIRECTION_SYMBOLS = ['>', 'v', '<', '^'] # Orientation vector key
VECTOR_COORDS = [(1, 0), (0, 1), (-1, 0), (0, -1)]
VECTORS = [Point(*v) for v in VECTOR_COORDS] # so we can retrieve by index
class Map():
""" 2D grid map. Follows 'move' instructions, which can either be a L/R rotation,
or n steps forward in the current orientation. If we step off a tile into the abyss,
we wrap around to the opposite edge. Stores the path taken, and uses it to evaluate a total 'score'. """
def __init__(self, grid: list[str]) -> None:
self._grid = grid # store original input grid
self._height = len(self._grid)
self._width = max(len(line) for line in self._grid) # the widest line
self._grid = self._pad_grid() # make all rows same length
self._cols = self._generate_cols()
self._staert = Point(0,0)
self._posn = Point(0,0)
self._direction = 0
self._path = {} # key=point, value=direction
self._set_start() # Initialise top-left, pointing right
self._last_instruction = "" # just to help with debugging
def _generate_cols(self):
""" Create a list of str, where each str is a column.
E.g. first col could be ' .... '
"""
cols_list = list(zip(*self._grid))
return ["".join(str(char) for char in col) for col in cols_list]
def _set_start(self):
""" Start position is first open space on the grid,
starting at (0, 0) - which could be in 'emtpy' space, and moving right. """
first_space = self._grid[0].find(".")
self._posn = Point(first_space, 0)
self._start = self._posn
self._direction = 0 # index of ['>', 'v', '<', '^']
self._path = {self._posn: self._direction} # Everywhere we've been, including direction
def _pad_grid(self):
""" Make all rows are the same length. """
return [line + " " * (self._width - len(line)) if len(line) < self._width else line for line in self._grid]
@property
def posn(self) -> Point:
""" Point coordinate of the current position. """
return self._posn
def move(self, instruction: str):
""" Can be direction instruction, i.e. L or R, or a move forward instruction, e.g. 10 """
self._last_instruction = instruction
if instruction.isdigit():
self._move_forward(int(instruction))
else:
self._change_direction(instruction)
def _change_direction(self, instruction):
""" Rotate to the left or the right, relative to current orientation. """
change = 1 if instruction == "R" else 3 # add 3 rather than -1, to avoid negative mod
self._direction = (self._direction+change) % len(VECTORS)
self._path[self._posn] = self._direction # update direction in the path
def _move_forward(self, steps: int):
""" Move in the current direction until we hit an obstacle. """
for _ in range(steps):
candidate, new_dir = self._next_posn()
if self._is_possible(candidate):
self._posn = candidate
self._direction = new_dir
self._path[self._posn] = self._direction # update direction in path
else: # we need to stop here
break
def _get_row_length(self, row_num: int):
return len(self._grid[row_num]) - self._grid[row_num].count(" ")
def _get_col_length(self, col_num: int):
return len(self._cols[col_num]) - self._cols[col_num].count(" ")
def _next_posn(self) -> tuple[Point, int]:
""" Determine next Point in this direction, including wrapping. Does not check if blocked. """
next_posn = self._posn + VECTORS[self._direction]
if not self._is_tile(next_posn): # we're off the tiles, so we need to wrap
# Subtract vector in the opposite direction equal to the length of the row / col
new_x = next_posn.x - VECTORS[self._direction].x * self._get_row_length(self._posn.y)
new_y = next_posn.y - VECTORS[self._direction].y * self._get_col_length(self._posn.x)
next_posn = Point(new_x, new_y)
return next_posn, self._direction
def _is_tile(self, point: Point) -> bool:
""" Check if the specified point is a tile. I.e. within the bounds and not empty. """
if point.y < 0 or point.y >= len(self._grid):
return False
# check not outside the bounds of the current row. (Allow for variable length row)
if point.x < 0 or point.x >= len(self._grid[point.y]):
return False
# If we've got this far, we're within the bounds of the input data, but it could still be empty
if self._get_value(point) == " ":
return False
return True
def _get_value(self, point: Point) -> str:
""" The value of the grid at the specified point. """
return self._grid[point.y][point.x]
def _is_possible(self, locn: Point):
""" Check if this space is open. Only '.' counts as open. """
return True if self._get_value(locn) == "." else False
def score(self) -> int:
""" Score is given by sum of: (1000*y), (4*x), facing.
For this calculation, x and y are 1-indexed. Facing = direction index. """
return 1000*(self.posn.y+1) + 4*(self.posn.x+1) + self._direction
def __str__(self) -> str:
lines = []
for y, row in enumerate(self._grid):
line = ""
for x, val in enumerate(row):
posn = Point(x,y)
if posn == self._posn:
line += (Colours.RED.value + Colours.BOLD.value
+ DIRECTION_SYMBOLS[self._path[posn]] + Colours.RESET.value)
elif posn == self._start:
line += (Colours.YELLOW.value + Colours.BOLD.value
+ DIRECTION_SYMBOLS[self._path[posn]] + Colours.RESET.value)
elif posn in self._path:
line += Colours.CYAN.value + DIRECTION_SYMBOLS[self._path[posn]] + Colours.RESET.value
else:
line += val
lines.append(line)
return "\n".join(lines)
def __repr__(self):
return f"Map(posn={self.posn}, last_instr={self._last_instruction}, score={self.score()})"
class CubeMap(Map):
""" Take a 2D grid that is made up of 6 regions, and convert to a cube.
The face coordinates of the Cube, and its edge mappings, must be supplied. """
def __init__(self, grid: list[str], face_coords: list[tuple], face_edge_map: dict[tuple, tuple]) -> None:
super().__init__(grid)
self._face_coords = face_coords # the coordinates of the top-left vertices of this cube
self._face_edge_map = face_edge_map
self._h_faces_width = max(x for x,y in self._face_coords) + 1 # e.g. 4 faces wide
self._v_faces_height = max(y for x,y in self._face_coords) + 1 # e.g. 3 faces tall
self._face_width = self._width // self._h_faces_width # E.g. 4, or 50 with real
self._face_height = self._height // self._v_faces_height # E.g. 4 or 50 with real"
assert self._face_width == self._face_height, "Faces should be squares!"
def _origin_face(self) -> int:
""" Get the face number (index) that this point lives in """
face_x = self._posn.x // self._face_width
face_y = self._posn.y // self._face_width
return self._face_coords.index((face_x, face_y))
def _next_posn(self) -> tuple[Point, int]:
""" Determine next Point in this direction, including wrapping. Does not check if blocked. """
next_posn = self._posn + VECTORS[self._direction]
next_dir = self._direction
if not self._is_tile(next_posn):
# we're off the tiles, so we need to wrap around the cube
next_posn, next_dir = self._next_face_point()
return next_posn, next_dir
def _next_face_point(self) -> tuple[Point, int]:
""" A face point is an x,y point within the current face only.
We return the new face point, and the new direction we're pointing in,
having changed face. """
dest_face, dest_direction = self._face_edge_map[(self._origin_face(), self._direction)]
# print(f"Moving to face {dest_face}, with direction={DIRECTION_SYMBOLS[dest_direction]}")
current_face_x = self.posn.x % self._face_width
current_face_y = self.posn.y % self._face_height
other = 0
dest_face_point = Point(0,0)
match self._direction: # which way are we currently going?
case 0: # >
assert current_face_x == self._face_width - 1, "We must be on a right edge"
other = current_face_y
case 1: # v
assert current_face_y == self._face_height - 1, "We must be on a bottom edge"
other = self._face_width - 1 - current_face_x
case 2: # <
assert current_face_x == 0, "We must be on a left edge"
other = self._face_height - 1 - current_face_y
case 3: # ^
assert current_face_y == 0, "We must be on a top edge"
other = current_face_x
match dest_direction: # which way will we be going?
case 0: # >
dest_face_point = Point(0, other)
case 1: # v
dest_face_point = Point(self._face_height - 1 - other, 0)
case 2: # <
dest_face_point = Point(self._face_height - 1, self._face_width - 1 - other)
case 3: # ^
dest_face_point = Point(other, self._face_width - 1)
# convert face point to grid point
return (self._face_point_to_grid_point(dest_face_point, dest_face), dest_direction)
def _face_point_to_grid_point(self, face_point: Point, face: int) -> Point:
""" Converts a point relative to a face back to an overall grid point. """
return Point(face_point.x + self._face_coords[face][0]*self._face_width,
face_point.y + self._face_coords[face][1]*self._face_height)
def main():
with open(INPUT_FILE, mode="rt") as f:
map_data, instructions = f.read().split("\n\n") # input is two blocks, separated by a line
with open(INPUT_CUBE, mode="rt") as f: # read in Cube input, in Python list format
cube_data = literal_eval(f.read())
map_data = map_data.splitlines()
# Part 1 - 2D map
the_map = Map(map_data)
process_instructions(instructions, the_map)
# print(the_map)
print(f"Part 1: score={the_map.score()}")
# Part 2 - Cube
cube = CubeMap(map_data, face_coords=cube_data[0], face_edge_map=cube_data[1])
process_instructions(instructions, cube)
print(f"Part 2: score={cube.score()}")
def process_instructions(instructions, the_map):
next_transition = 0
this_instr = ""
for i, char in enumerate(instructions):
if i < next_transition:
continue
if char.isdigit():
for j, later_char in enumerate(instructions[i:len(instructions)], i):
if not later_char.isdigit():
next_transition = j
this_instr = instructions[i: next_transition]
break
else: # we've reached the end
this_instr = instructions[i]
else: # we're processing alphabetical characters
this_instr = instructions[i]
the_map.move(this_instr)
if __name__ == "__main__":
t1 = time.perf_counter()
main()
t2 = time.perf_counter()
print(f"Execution time: {t2 - t1:0.4f} seconds")
And the output looks like this:
Part 1: score=27436
Part 2: score=15426
Execution time: 0.0646 seconds