The Python Journey - Sets

Useful Links

Sets are really useful when we want to store a number of unique items, but we don’t care about the order of those items.

Python sets have these attributes:

They cannot contain duplicate items. Adding a duplicate item simply does nothing.
The items in the set must be immutable. I.e. objects that can’t be modified and which are hashable. For this reason, it can be extremely convenient to use the dataclass when defining your own objects for use in sets, with the frozen=True attribute set.
Items in the set are unordered. Thus, items are not indexable. (Though, if you want an ordered set, you can create your own implementation.)

You should consider using sets whenever you need to:

Count how many items in a collection are unique.
Perform set algebra, such as:
- Determine if an object already exists in another set (membership).
- Determine which items overlap, across two different sets.

Quick Demo

from dataclasses import dataclass

@dataclass(frozen=True)
class Point():
    """ Point class, which stores x and y """
    x: int
    y: int
    
point_a = (5, 10)
point_b = (6, 5)
point_c = (5, 10)   # this is a duplicate (non-unique) point
point_d = (20, 30)

points = set()
points.add(point_a)
points.add(point_b)
points.add(point_c)

print(f"Points contains {len(points)} points.")   # We've only added 2 unique points

print(f"Point c is in points? {point_c in points}")  # Because c and a are actually the same
print(f"Point d is in points? {point_d in points}")  # We haven't added this

# We can make a points list like this...
points_list = [point_a, point_b, point_c, point_d]  # 4 items
print(f"Points_list contains {len(points_list)} points.")   # still four items
print(f"Points_list: {points_list}")

# And now we can convert it to a set
# This is a convenient way to strip out duplicates from any collection!
points_set = set(points_list)
print(f"Points_set contains {len(points_set)} points.")   # now 3 items
print(f"Points_set: {points_set}")

Output:

Points contains 2 points.
Point c is in points? True
Point d is in points? False
Points_list contains 4 points.
Points_list: [(5, 10), (6, 5), (5, 10), (20, 30)]
Points_set contains 3 points.
Points_set: {(5, 10), (20, 30), (6, 5)}

Set Algebra

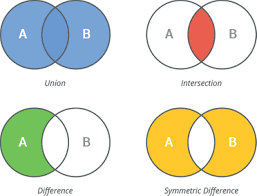
Mathematical set algebra is easily achieved using Python sets. For example, we can use set algebra to determine when one set contains another set, any intersection of sets, any difference between sets, and any union that is created by combining sets. If you’re unfamiliar with set theory, but you understand Venn diagrams, then guess what… You pretty much understand set theory!

Set Relationship	Looks like
Union (\|)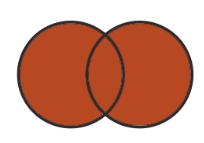
Intersection (&)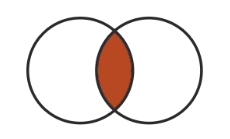
Difference (-)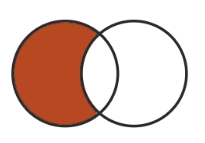
Symmmetric Difference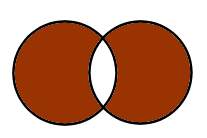
Superset/Contains (>)
Subset (<)

‹›