Advent of Code 2015 - Day 13

Useful Links

Concepts and Packages Demonstrated

regex Permutations and Combinations Graphs Defaultdict Lambda Functions Graphs with NetworkX Typing and Type Hinting Collections.abc

Problem Intro
Part 1
Part 2
Solving with NetworkX
- Drawing the Graph

Problem Intro

We’re given a list of people who will sit around a round table. We’re asked to find the optimum seating arrangement, based on total happiness. Each person will be sat between two other people. People gain or lose happiness points, depending on who they are sat next to.

The input looks like this:

Alice would gain 54 happiness units by sitting next to Bob.
Alice would lose 79 happiness units by sitting next to Carol.
Alice would lose 2 happiness units by sitting next to David.
Bob would gain 83 happiness units by sitting next to Alice.
Bob would lose 7 happiness units by sitting next to Carol.
Bob would lose 63 happiness units by sitting next to David.
Carol would lose 62 happiness units by sitting next to Alice.
Carol would gain 60 happiness units by sitting next to Bob.
Carol would gain 55 happiness units by sitting next to David.
David would gain 46 happiness units by sitting next to Alice.
David would lose 7 happiness units by sitting next to Bob.
David would gain 41 happiness units by sitting next to Carol.

Part 1

What is the total change in happiness for the optimal seating arrangement of the actual guest list?

The real input data doesn’t have that many people. There’s only 8 people. And so, there are only 8! = 40320 different ways to order these 8 people. In modern day computing, this is nothing!

We can treat the arrangement of people as an weighted directed graph, also known as a weighted digraph. I.e.

Each person is a node in the graph.
The edges have magnitude, where the magnitude is the happiness that person A gets by sitting next to person B.
It is a directed graph, because the magnitude of the edge from A to B will be different from the magnitude of the edge from B to A. Or, to put it another way, A may like B, but B might hate A!

As with similar undirected graph challenges, we can use a solution something like…

Use regex to extract the happiness scores in each direction.
Build an adjacency list to store the happiness score for each adjacent pair.
Determine all 40000-ish arrangements (permutations) of the 8 people.
Calculate the sum of happiness for each arrangement.

First, let’s look at the function that creates our adjacency list, to get the happiness score for any pair of people:

def get_happiness_by_person(data) -> dict[str, dict[str, int]]:
    """ Here we build an adjacency list.  We will map each person to every other person.
    Since this is a directed graph, we'll use a defaultdict(dict).

    Args:
        data (list): A list of happiness statements

    Returns:
        dict: dict[person_x][person_y: happiness]
    """
    # Alice would gain 54 happiness units by sitting next to Bob.
    happiness = defaultdict(dict)
    happiness_pattern = re.compile(r"^(\w+) would (\w+) (\d+) happiness units by sitting next to (\w+)")
    
    for line in data:
        person_1, gain_or_lose, value, person_2 = happiness_pattern.findall(line)[0]
        if gain_or_lose == "gain":
            value = int(value)
        else:
            value = -(int(value))
    
        happiness[person_1][person_2] = value

    return happiness

This code:

Uses regex to extract the names and happiness values from each statement. Nothing new here.
Determines with the person gains or loses happiness, and sets the value to positive or negative, accordingly.
We then use a defaultdict that sets the key to a person A, and then sets the value to an empty (default) dict. For each person B, we set add a key of person B and set the value to be the happiness score.

Having built our adjacency list, we create set of all the people in our data:

    # build up a dict of hapiness scores for each person
    happiness_by_person = get_happiness_by_person(data)

    # create a set of all the people
    people = set(happiness_by_person.keys())

Now we want to determine the first person. Because everyone is sat in a circle, we can arbitrarily choose someone to be the head of the table. All our seating permutations will assume this starting position. By restricting the first person to always be the same person, we dramatically reduce the number of permutations we need to work through. That’s because there’s one fewer persons in our set of people to establish permutations for.

If we didnt’ fix the first position, we would have to work through 8! = 40320 permutations. But by fixing the position of person 1, there are now only 7 remaining people to calculate permuations for. And 7! = 5040.

    # we don't care where the first person sits, since it's a circle.  
    # So let's just make person_1 the 'head' of the table
    person_1 = people.pop()

    # get all permutations for remaining people around the table, as list of tuples
    # We expect n! perms
    perms = list(permutations(people))

Finally, we can determine the total happiness score for each of our permutations:

    happiness_for_seating = {}
    for perm in perms:
        # this allows us to remove reverse permutations
        if perm <= perm[::-1]:
            perm = list(perm)  # convert perm from tuple to list, to make it mutable
            perm.insert(0, person_1) # such that we can insert the head of the table

            # now convert back to tuple to make it hashable. Otherwise we can't use it as dict key
            happiness_for_perm[tuple(perm)] = compute_happiness_for_perm(perm, happiness_by_person)

It works like this:

We create a dict to map each permutation against a total happiness score.
We iterate through each of our permutations. Recall that with one fixed position and 7 remaining positions, we only have 5040 permutations to work through.
We then add another efficiency: we skip reverse permutations.
- E.g. if we had a sequence ABCDEF, then we would ignore a sequence FEDCBA. Because, for people sat around a table, these are the same.
- How do we do this? Easy! We check if our current permutation is less than the reverse permutation, using the [::-1] construct to return the reversed list. We only go with the permutation that is arbitrarily the smaller one.
We now must add back in our head of the table to our current permutation. Remember that this person was previously excluded, when the permutations were calculated. We do this by using the insert() method to insert this person at the front of the list.
Then we compute the total happiness for this arrangement. Here’s the code that achieves this:

def compute_happiness_for_seating(seating_arrangement, happiness_by_person):
    happiness = 0

    for i, current_person in enumerate(seating_arrangement):
        if i < len(seating_arrangement) - 1:
            current_next_person = seating_arrangement[i+1]
        else:
            current_next_person = seating_arrangement[0]

        happiness += happiness_by_person[current_person][current_next_person]
        happiness += happiness_by_person[current_next_person][current_person]

    return happiness

This works by iterating over each person in our list of people, determining who the next (adjacent) person is, and retrieving the happiness score (relative to the first person) from our adjacently dictionary. Note that if we’ve reached the last person in our list, the code then sets the next person to be the first person in the list. This works, because they are sat in a circle.

Having now built up a dictionary that maps each permutation to a total score, we’re finally able to determine the permutation with the highest score.

    optimum_happiness_seating = max(happiness_for_seating.items(), key=lambda x: x[1])[0]
    print("Part 1")
    print(f"Optimum happiness = {happiness_for_seating[optimum_happiness_seating]} with seating: {optimum_happiness_seating}")

The use of max() is interesting. Here’s how it works:

We pass in our dict of perm:score as the first parameter, and using the dict’s items() method, which returns all the dict K:V pairs as a tuple.
We then set the key for our max() function to be a lambda function that simply returns the second value from each tuple, i.e. the happiness total.

This is how we tell max() to retrieve the largest value, based on the dict value, rather than based on the dict key.

And that’s it!

Part 2

Now we’re told we need to insert ourselves in the seating arrangement. We’re told we’re ambivalent about who we sit next to, and they’re ambivalent about us. I.e. the happiness score will be 0 in both directions, for anyone we’re sat next to.

What is the total change in happiness for the optimal seating arrangement that actually includes yourself?

To solve this:

Add person 1 - the head of the table - back in to the set of people.
Extend the adjacency dictionary, by adding me as a neighbour to each other person.
Once again, remove person 1 as the head of the table.
Add me to the set of people.

And then we can simply repeat the same code as in Part 1.

After a bit of refactoring, the final solution looks like this:

""" 
Author: Darren
Date: 12/02/2021

Solving https://adventofcode.com/2015/day/13

A list of people sat around the table.
Happiness scores depend on who sets next to whom. E.g.
    Alice would gain 54 happiness units by sitting next to Bob.

Solution:
    Use a defaultdict to store happiness scores each person.  E.g.
        happiness[Alice][Bob] = 54
    
    Use a set to store all people.
    Find all permutations of people around the table using itertools.permutations().
    Create a dict happiness_for_perms
    For each perm:
        We don't want to process reverse order of perms, so check using <= vs last element
        For each person around the table clockwise:
            Add up the happiness of the adjacent people
        Store happiness for this perm

Part 1:
    Find happiness of optimal seating arrangement

Part 2:
    Add myself, and assume that all happiness relationships are 0, wherever I go.
    
    Add myself to the dict for every other person in the set.
    Add me to the set.
    Repeat Part 1.
"""
import os
import time
import re
from itertools import permutations
from collections import defaultdict
from operator import itemgetter

SCRIPT_DIR = os.path.dirname(__file__) 
INPUT_FILE = "input/input.txt"
# INPUT_FILE = "input/sample_input.txt"

def main():
    input_file = os.path.join(SCRIPT_DIR, INPUT_FILE)
    with open(input_file, mode="rt") as f:
        data = f.read().splitlines()

    print("Part 1")
    # build up a dict of hapiness scores for each person
    happiness_by_person = get_happiness_by_person(data)

    # create a set of all the people
    people = set(happiness_by_person.keys())

    # we don't care where the first person sits, since it's a circle.  
    # So let's just make person_1 the 'head' of the table
    person_1 = people.pop()

    # get all permutations for remaining people around the table, as list of tuples
    # We expect n! perms
    happiness_for_perm, optimum_happiness_perm = find_optimum_happiness(happiness_by_person, person_1, people)
    print(f"Optimum happiness = {happiness_for_perm[optimum_happiness_perm]} with seating: {optimum_happiness_perm}")

    print("\nPart 2")
    # Need to add person_1 back in, so that we can add values for Me sitting next to Person_1
    people.add(person_1)
    add_me_to_happiness_by_person(happiness_by_person, people)
    people.remove(person_1)
    people.add('Me')

    happiness_for_perm, optimum_happiness_perm = find_optimum_happiness(happiness_by_person, person_1, people)
    print(f"Optimum happiness = {happiness_for_perm[optimum_happiness_perm]} with seating: {optimum_happiness_perm}")

def find_optimum_happiness(happiness_by_person, person_1, people):
    """ Determine all permutations of seating.
    Reduce number of perms by removing person_1.
    Compute happiness score for each permutation.
    Determine the permutation with the greatest happiness score.

    Args:
        happiness_by_person (dict): Happiness adjacency map
        person_1 (str): Arbitrary head of the table
        people (set): The people to seat around the table

    Returns:
        tuple: (score, optimum_seating_permutation)
    """
    perms = list(permutations(people))
    happiness_for_perm = {}
    for perm in perms:
        # this allows us to remove reverse permutations
        if perm <= perm[::-1]:
            perm = list(perm)  # convert perm from tuple to list, to make it mutable
            perm.insert(0, person_1) # such that we can insert the head of the table

            # now convert back to tuple to make it hashable. Otherwise we can't use it as dict key
            happiness_for_perm[tuple(perm)] = compute_happiness_for_perm(perm, happiness_by_person)
    
    optimum_happiness_perm = max(happiness_for_perm.items(), key=lambda x: x[1])[0]
    return happiness_for_perm, optimum_happiness_perm

def add_me_to_happiness_by_person(happiness_by_person: dict, people):
    for person in people:
        happiness_by_person[person]['Me'] = 0
        happiness_by_person['Me'][person] = 0

def compute_happiness_for_perm(seating_arrangement, happiness_by_person):
    happiness = 0

    for i, current_person in enumerate(seating_arrangement):
        if i < len(seating_arrangement) - 1:
            current_next_person = seating_arrangement[i+1]
        else:
            current_next_person = seating_arrangement[0]

        happiness += happiness_by_person[current_person][current_next_person]
        happiness += happiness_by_person[current_next_person][current_person]

    return happiness

def get_happiness_by_person(data) -> dict[str, dict[str, int]]:
    """ Here we build an adjacency list.
    We will map each person to every other person.
    Since this is a directed graph, we'll use a defaultdict(dict).

    Args:
        data (list): A list of happiness statements

    Returns:
        dict: dict[person_x][person_y: happiness]
    """
    # Alice would gain 54 happiness units by sitting next to Bob.
    happiness = defaultdict(dict)
    happiness_pattern = re.compile(r"^(\w+) would (\w+) (\d+) happiness units by sitting next to (\w+)")
    
    for line in data:
        person_1, gain_or_lose, value, person_2 = happiness_pattern.findall(line)[0]
        if gain_or_lose == "gain":
            value = int(value)
        else:
            value = -(int(value))
    
        happiness[person_1][person_2] = value

    return happiness

if __name__ == "__main__":
    t1 = time.perf_counter()
    main()
    t2 = time.perf_counter()
    print(f"Execution time: {t2 - t1:0.4f} seconds")

And my solution output looks like this:

Part 1
Optimum happiness = 664 with seating: ('Frank', 'Carol', 'Mallory', 'David', 'Alice', 'Bob', 'George', 'Eric')

Part 2
Optimum happiness = 640 with seating: ('Frank', 'Eric', 'George', 'Bob', 'Alice', 'David', 'Mallory', 'Carol', 'Me')
Execution time: 0.0438 seconds

Solving with NetworkX

NetworkX is a cool library that allows us to build a graph, and then solve problems with that graph. It can also be used to visualise our graph visually. So here, I’ve built a second solution using NetworkX.

First, let’s look at everything except visualising the graph:

from collections.abc import Iterable
from itertools import permutations
from pathlib import Path
import time
import re
import networkx as nx
import matplotlib.pyplot as plt

SCRIPT_DIR = Path(__file__).parent 
INPUT_FILE = Path(SCRIPT_DIR, "input/input.txt")

HAPPINESS = "happiness"
SHOW_GRAPH = True

def main():
    with open(INPUT_FILE, mode="rt") as f:
        data = f.read().splitlines()

    graph = build_graph(data)

    print("\nPart 1")
    people = set(graph.nodes.keys())
    person_a = people.pop()
    
    max_happiness = get_seating_with_max_happiness(graph, people, person_a)
    print(f"Optimum happiness: {max_happiness}")
    
    print("\nPart 2")
    # Need to add person_a back in, so that we can add values for Me sitting next to person_a
    people.add(person_a)
    graph = add_me_to_happiness_by_person(graph)
    people = set(graph.nodes.keys())
    people.remove(person_a)

    max_happiness = get_seating_with_max_happiness(graph, people, person_a)
    print(f"Optimum happiness: {max_happiness}")
    
    if SHOW_GRAPH:
        draw_graph(graph, max_happiness[0])

def get_seating_with_max_happiness(graph, people, person_a):
    happiness_for_perm = {}
    for perm in permutations(people): # E.g. for route ABC     
        # Use path_weight to get the total of all the edges that make up the route
        if perm <= perm[::-1]:
            perm = list(perm)
            perm.insert(0, person_a)
            perm.append(person_a)
            
            # Get happiness in the first direction, e.g. person A -> B
            total_happiness_forward = nx.path_weight(graph, perm, weight=HAPPINESS)
            # Now get happiness in the reverse direction, e.g. person B -> A
            total_happiness_reverse = nx.path_weight(graph, perm[::-1], weight=HAPPINESS)
            
            # For total happiness for this seating arrangement, we need to add forward and reverse
            happiness_for_perm[tuple(perm)] = total_happiness_forward + total_happiness_reverse

    max_journey = max(happiness_for_perm.items(), key=lambda x: x[1])
    return max_journey
    
def build_graph(data: list) -> nx.DiGraph:
    """ 
    Build graph of of all people, including happiness scores between each person.
    """
    graph = nx.DiGraph()
    happiness_pattern = re.compile(r"^(\w+) would (\w+) (\d+) happiness units by sitting next to (\w+)")
    
    # Add each edge, in the form of a location pair
    for line in data:
        person_1, gain_or_lose, value, person_2 = happiness_pattern.findall(line)[0]
        if gain_or_lose == "gain":
            value = int(value)
        else:
            value = -(int(value))
            
        graph.add_edge(person_1, person_2, happiness=value)

    return graph

def add_me_to_happiness_by_person(graph: nx.DiGraph) -> nx.DiGraph:
    """ Extend the graph by adding "Me", 
    with happiness weight of 0 for all pairings that include Me.
    """
    people = list(graph.nodes()) # make a copy of the names
    
    for person in people:
        graph.add_edge(person, "Me", happiness=0)
        graph.add_edge("Me", person, happiness=0)
        
    return graph
    
if __name__ == "__main__":
    t1 = time.perf_counter()
    main()
    t2 = time.perf_counter()
    print(f"Execution time: {t2 - t1:0.4f} seconds")

Some notes about this code:

I’ve imported Collections.abc.Iterable, so that I can use Iterable in type hinting of draw_graph() function later.
As always, to use NetworkX, we need to import it, as well as matplotlib.pyplot for the visualisation.
We’ve defined a constant called HAPPINESS, which we can use as the key for our weight attribute. Remember that we’re working with a weighted directed graph, so edge edge needs a weight, and we can give this weight any name we like.
Our build_graph() function parses the input data using regex and creates a nx.DiGraph return value. The code here is almost identical to our get_happiness_by_person() function from the first solution, except that with each input line, we add the values to the graph using add_edge(), rather than adding the values to a defaultdict. Note how we use type hinting to tell our linter that the expected return value should be of type nx.DiGraph.
As before, we want a set of all the people around the table. Instead of pulling the keys from a defaultdict, we can pull the nodes from the graph.
As before, we pop() the first person from the set, in order to define the “head of the table”.
Now we want to find the optimum seating arrangement, which we do with the get_seating_with_max_happiness() function. This works nearly identically to our previous find_optimum_happiness() function, but with these differences:
- We create a happiness_for_perm dictionary, which will store each permutation as a key, and the total happiness for that permutation (by adding up happiness scores in both directions) as the value. Note that we have to turn the current permutation into a tuple before we use it as a key for the dictionary, because dictionaries require hashable objects as keys.
- When we add our “head of the table” back at the beginning of each permutation, we also add the same person at the end, to close the loop. Our networkx algorithm requires this.
- Then, instead of our own compute_happiness_for_perm() function to add up all the happiness scores in both directions, we can instead use nx.path_weight(), and pass in the current permutation as a path.
- We also have to pass the permutation in reverse, because we need to add up the happiness scores in both directions.
- We add the current seating permutation to our happiness_for_perm dict.
- Finally, we return the permutation with the max() happiness, just as we did before. Thus, Part 1 is solved.
For Part 2, we need to add me to the table. This works just as it did in the previous solution, except that we add me as two new edges, rather than as new dictionary items.

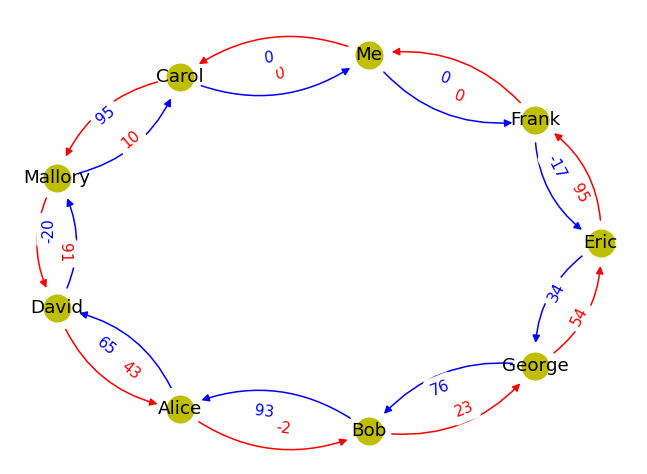
Drawing the Graph

Now let’s visualise it:

def draw_graph(graph: nx.DiGraph, arrangement: Iterable):
    """ Takes the original graph and a seating arrangement, 
    builds a new graph with the nodes in the correct arrangement order, and draws it.
    """
    # Get the edges from only the adjacent people in our seating arrangement
    edges = list(nx.utils.pairwise(arrangement))
    
    # Get dict of {(A, B): happiness} to use as edge labels
    edge_labels = {(person_1, person_2): graph[person_1][person_2][HAPPINESS] 
                        for (person_1, person_2) in edges}
    
    # Get dict of {(B, A): happiness}
    reverse_edges = [(b, a) for a, b in edges] # to use as edge labels
    reverse_edge_labels = {(person_2, person_1): graph[person_2][person_1][HAPPINESS] 
                        for (person_1, person_2) in edges}
    
    all_edges = edges + reverse_edges # a single list of all edges, in both directions
    
    seating_graph = nx.DiGraph() # Create a new graph, to which we will add only relevant edges
    for (person_1, person_2) in all_edges:
        happiness_score = graph[person_1][person_2][HAPPINESS]
        seating_graph.add_edge(person_1, person_2, happiness=happiness_score)

    pos = nx.circular_layout(seating_graph) # arrange our nodes - in the right order - in a circle
   
    # Nodes and node labels
    nx.draw_networkx_nodes(seating_graph, pos, node_color="y")
    nx.draw_networkx_labels(seating_graph, pos, font_family="sans-serif")
    
    # Edges - use arc3 to curve them, otherwise we end up with a double-arrowed line
    nx.draw_networkx_edges(seating_graph, pos, edgelist=edges, # forward edges
                           width=1, edge_color="r", connectionstyle='arc3, rad = 0.3', 
                           min_source_margin=15, min_target_margin=15)
    nx.draw_networkx_edges(seating_graph, pos, edgelist=reverse_edges, # reverse edges
                           width=1, edge_color="b", connectionstyle='arc3, rad = 0.3', 
                           min_source_margin=15, min_target_margin=15)
    
    # Edge weight labels
    nx.draw_networkx_edge_labels(seating_graph, pos, edge_labels, 
                                 font_color="r", verticalalignment="top", horizontalalignment="left")
    nx.draw_networkx_edge_labels(seating_graph, pos, reverse_edge_labels, 
                                 font_color="b", verticalalignment="bottom", horizontalalignment="right")
    
    ax = plt.gca()
    plt.axis("off")
    plt.tight_layout()
    plt.show()

The code is well documented, so you should be able to follow it.

Our final output looks something like this:

Part 1
Optimum happiness: (('Carol', 'Frank', 'Eric', 'George', 'Bob', 'Alice', 'David', 'Mallory', 'Carol'), 664)

Part 2
Optimum happiness: (('Carol', 'Mallory', 'David', 'Alice', 'Bob', 'George', 'Eric', 'Frank', 'Me', 'Carol'), 640)
Execution time: 1.2427 seconds

And it draws a visualisation that looks like this:

Day 13 Seating Arrangement Vis!

‹›

Learning Python with Advent of Code Walkthroughs