Learning Python with Advent of Code Walkthroughs

Dazbo's Advent of Code solutions, written in Python

Wires and Gates

Advent of Code 2015 - Day 9

Day 9: All in a Single Night

Useful Links

‹›

Concepts and Packages Demonstrated

Travelling Salesman ProblemGraphsregexpermutationsNetworkX

Page Navigation

Problem Intro

We’re told that Santa needs to visit every location on his list exactly once. The distances between all pairs of locations have been provided, in the form of data that looks like this:

London to Dublin = 464
London to Belfast = 518
Dublin to Belfast = 141

Part 1

Starting at any location and ending at any location, what is the shortest distance that Santa must travel to visit every location exactly once?

This is actually a fairly standard problem, known as the Travelling Salesman Problem.

My strategy is as follows:

After we’ve obtained the total distance for each permutation, we simply need to find the shortest distance. This is trivial, since we can just use the min() function and pass in our list of distances.

The code looks like this:

from pathlib import Path
import time
import re
from itertools import permutations

SCRIPT_DIR = Path(__file__).parent 
INPUT_FILE = Path(SCRIPT_DIR, "input/input.txt")
# INPUT_FILE = Path(SCRIPT_DIR, "input/sample_input.txt")

def main():
    with open(INPUT_FILE, mode="rt") as f:
        data = f.read().splitlines()

    locs_to_distances = get_distances(data) # E.g. (A, B) = n
    
    # build our set of unique locations
    locations = set()
    for loc_pair in locs_to_distances:
        locations.add(loc_pair[0]) # place_a
        locations.add(loc_pair[1]) # place_b

    journey_distances = [] # store total journey distances

    # Create permutations of all possible combinations of locations
    # I.e. all possible ways of ordering the locations we must visit.
    # E.g. if we have to visit places A, B and C, there would be 3! perms:
    # ABC, ACB, BAC, BCA, CAB, CBA
    for loc_perm in permutations(locations):
        # For efficiency: filter out inverse routes. E.g. we want ABC, but not CBA; they are the same
        if loc_perm[0] < loc_perm[-1]: 
            journey_dist = 0
            for i in range(len(loc_perm)-1):
                # iterate through location pairs i, i+1, for all locations in this permutation
                # E.g. for A, B, C, we would have pairs: A-B, and B-C.
                pair_a = loc_perm[i]
                pair_b = loc_perm[i+1]
                dist = locs_to_distances[(pair_a, pair_b)]
                journey_dist += dist
            
            # Just store the total distance for this journey.
            # If we cared about the order of places, we could use a dict and store those too
            journey_distances.append(journey_dist)

    print(f"Shortest journey: {min(journey_distances)}")

def get_distances(data) -> dict:
    """ Read list of distances between place_a and place_b.
    Return dict that maps (A,B)->dist x, and (B,A)->dist x.

    Args:
        data (list[str]): distances, in the form "London to Dublin = 464"

    Returns:
        dict: (start, end) = distance
    """
    distances = {}
    distance_match = re.compile(r"^(\w+) to (\w+) = (\d+)")
    
    for line in data:
        start, end, dist = distance_match.findall(line)[0]
        dist = int(dist)

        # create a distance record in the form: [(loc_1, loc_2), dist]
        # And also store it in reverse, so that when we look it up, 
        # it doesn't matter which order the locations come in the journey.
        distances[(start, end)] = dist
        distances[(end, start)] = dist

    return distances

if __name__ == "__main__":
    t1 = time.perf_counter()
    main()
    t2 = time.perf_counter()
    print(f"Execution time: {t2 - t1:0.4f} seconds")

Simples!

Part 2

I love it when we get a Part 2 like this!

We’re told that Santa wants to show off and take the route with the longest distance. Our code only needs one extra line of code! We just add this:

    print(f"Longest journey: {max(journey_distances)}")

The final output is:

Shortest journey: 207
Longest journey: 804
Execution time: 0.0460 seconds

That’s pretty swift!

Solving with NetworkX

NetworkX is a cool library that allows us to build a graph, and then solve problems with that graph, e.g. shortest and longest path between two points. It can also be used to visualise our graph visually.

Here’s a solution using NetworkX…

from itertools import permutations
from pathlib import Path
import time
import re
import networkx as nx
import matplotlib.pyplot as plt

SCRIPT_DIR = Path(__file__).parent 
INPUT_FILE = Path(SCRIPT_DIR, "input/input.txt")
# INPUT_FILE = Path(SCRIPT_DIR, "input/sample_input.txt")

DISTANCE = "distance"

SHOW_GRAPH = True

def main():
    with open(INPUT_FILE, mode="rt") as f:
        data = f.read().splitlines()

    graph = build_graph(data)

    locations = graph.nodes
    journey_distances = {}

    for route in permutations(locations): # E.g. for route ABC     
        # Use path_weight to get the total of all the edges that make up the route
        route_distance = nx.path_weight(graph, route, weight=DISTANCE)
        journey_distances[route] = route_distance

    # Get (journey, distance) tuples
    min_journey = min(journey_distances.items(), key=lambda x: x[1])
    max_journey = max(journey_distances.items(), key=lambda x: x[1])
    
    print(f"Shortest journey: {min_journey}")
    print(f"Longest journey: {max_journey}")
    
    if SHOW_GRAPH:
        draw_graph(graph, min_journey[0])  
        draw_graph(graph, max_journey[0])
    
def draw_graph(graph, route):
    start_node = route[0]
    end_node = route[-1]
    
    pos = nx.spring_layout(graph) # create a layout for our graph

    # Draw all nodes in the graph
    nx.draw_networkx_nodes(graph, pos, 
                           nodelist=route[1:-1], # exclude start and end
                           node_color="green")
    
    # Draw all the node labels
    nx.draw_networkx_labels(graph, pos, font_size=11)
    
    # Draw start and end nodes
    nx.draw_networkx_nodes(graph, pos, nodelist=[start_node], 
                           node_color="white", edgecolors="green")
    nx.draw_networkx_nodes(graph, pos, nodelist=[end_node], 
                           node_color="orange", edgecolors="green")

    # Draw closest edges for each node only - with thin lines
    nx.draw_networkx_edges(graph, pos, 
                           edge_color="green", width=0.5)
    
    # Draw all the edge labels - i.e. the distances
    nx.draw_networkx_edge_labels(graph, pos, nx.get_edge_attributes(graph, DISTANCE))
    
    # Draw the edges that make up this particular route
    route_edges = list(nx.utils.pairwise(route))
    nx.draw_networkx_edges(graph, pos, edgelist=route_edges,
                           edge_color="red", width=3, arrows=True)
    
    ax = plt.gca()
    plt.axis("off")
    plt.tight_layout()
    plt.show()    
    
def build_graph(data) -> nx.Graph:
    """ Read list of distances between place_a and place_b.
    Return dict that maps (A,B)->dist x, and (B,A)->dist x.

    Args:
        data (list[str]): distances, in the form "London to Dublin = 464"

    Returns:
        dict: (start, end) = distance
    """
    graph = nx.Graph()
    distance_match = re.compile(r"^(\w+) to (\w+) = (\d+)")
    
    # Add each edge, in the form of a location pair
    for line in data:
        start, end, distance = distance_match.findall(line)[0]
        distance = int(distance)
        graph.add_edge(start, end, distance=distance)

    return graph

if __name__ == "__main__":
    t1 = time.perf_counter()
    main()
    t2 = time.perf_counter()
    print(f"Execution time: {t2 - t1:0.4f} seconds")

Some things to note about this code:

The output looks like this:

Shortest journey: (('Norrath', 'Straylight', 'Arbre', 'Faerun', 'AlphaCentauri', 'Snowdin', 'Tambi', 'Tristram'), 207)
Longest journey: (('Tambi', 'Faerun', 'Norrath', 'Tristram', 'AlphaCentauri', 'Arbre', 'Snowdin', 'Straylight'), 804)
Execution time: 0.4862 seconds

This clearly runs a lot slower than my first solution. But it saved us some code, and makes it really easy to draw the graph…

Drawing the Graph

One cool thing about NetworkX is that it’s really easy to render a visual representation of our graph. In the code above you’ll see that I’ve explicitly done the following things:

The resulting graphs look like this:

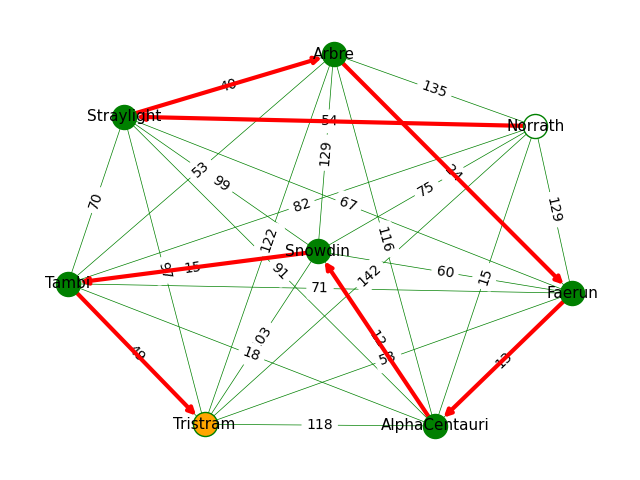
Shortest Path
Shortest Path
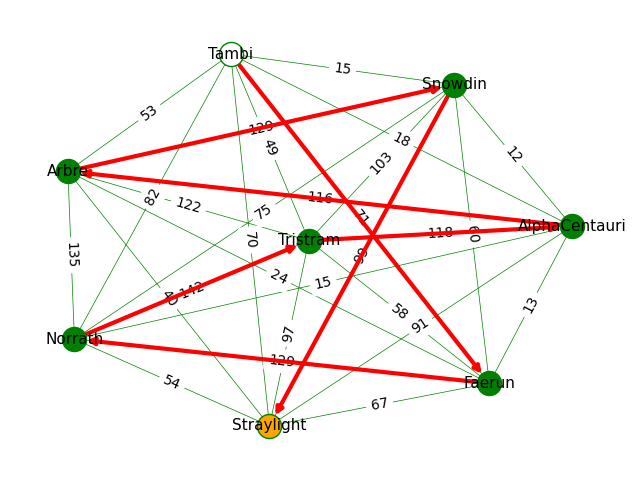
Longest Path
Longest Path

Cool, right?

‹›