Advent of Code 2021 - Day 22

Day 22: Reactor Reboot

Useful Links

‹›

• 2021 Main Page
• My solution code

Concepts and Packages Demonstrated

Regular expressionsbisect_lefttqdm

Coordinate compressionProgress Bar

Problem Intro

I’ve got to admit… At this point in my 2021 AoC journey, I was starting to feel a little grumpy about how much time these challenges were taking. My original expectation was that I’d have most days done by breakfast, and there might be one or two tough days. But at this point, I’m writing off half my annual leave to solving AoC problems. Urgh.

For me, this was one of the toughest challenges. It was hard to get my head around how to solve it. And it was hard to turn my idea into code.

Anyhoo…

We’re told we need to reboot the sub’s reactor. And the reactor is made up of a massive 3D grid of one-unit cubes, where cubes can be on or off.

We need to follow a reboot sequence, which is a set of on or off instructions, which each instruction followed by x, y, and z ranges that describe a cuboid. I.e. an on instruction will turn all the cubes on, in the 3D cuboid region described by the instruction. And, obviously, an off instruction will turn them all off.

Our sample input looks like this:

on x=-5..47,y=-31..22,z=-19..33
on x=-44..5,y=-27..21,z=-14..35
on x=-49..-1,y=-11..42,z=-10..38
on x=-20..34,y=-40..6,z=-44..1
off x=26..39,y=40..50,z=-2..11
on x=-41..5,y=-41..6,z=-36..8
off x=-43..-33,y=-45..-28,z=7..25
on x=-33..15,y=-32..19,z=-34..11
off x=35..47,y=-46..-34,z=-11..5
on x=-14..36,y=-6..44,z=-16..29
on x=-57795..-6158,y=29564..72030,z=20435..90618

Part 1

Considering only cubes in the region x=-50..50,y=-50..50,z=-50..50, how many cubes are on after following the reboot sequence?

It’s pretty obvious what Part 2 is going to say. <sigh>

Well, I started off by doing it the obvious way, hoping (foolishly) that it might scale for Part 2.

Setup

from __future__ import annotations
import logging
import os
import time
import re
from typing import NamedTuple
from bisect import bisect_left
from tqdm import tqdm

logging.basicConfig(format="%(asctime)s.%(msecs)03d:%(levelname)s:%(name)s:\t%(message)s", 
                    datefmt='%H:%M:%S')
logger = logging.getLogger(__name__)
logger.setLevel(logging.DEBUG)

SCRIPT_DIR = os.path.dirname(__file__) 
INPUT_FILE = "input/input.txt"
# INPUT_FILE = "input/sample_input.txt"

A couple of things we haven’t used before in this AoC:

• bisect.bisect_left - a useful package and method for working with sorted lists
• tqdm - an awesome package that can turn any loop into a dynamic progress bar!

class Instruction(NamedTuple):
    """ An instruction to turn on/off all the cubes in the region described by the Cuboid """
    on_or_off: str
    cuboid: Cuboid

class Cuboid(NamedTuple):
    """ Stores the x, y and z coordinates that make up a cuboid. """
    x_range: tuple[int, int]
    y_range: tuple[int, int]
    z_range: tuple[int, int]

Not much to say about that. I’m using a NamedTuple for both the Instruction class, and for the Cuboid class. This just makes them a bit more readable.

Now I’ll create a class that reprents the Reactor:

class Reactor():
    """ 3D space that contains a number of unit cubes. Initially, all cubes are turned off.
    We process a number of instructions, which toggles cuboid regions to be on or off. """
    
    def __init__(self, bound:int=0) -> None:
        """ Initialise this cuboid set.  When adding / subtracting points (later), ignore anything out of bounds. 
        Bound is given by (0-bound, 0+bound) in any dimension. 0 means no bound. """
        self._bound = bound
        self._cuboid = set()
        
    @property
    def cubes_on(self):
        return len(self._cuboid)
    
    def update(self, instr:Instruction):
        """ Turn on / off points that are supplied in the form of a Cuboid. """
        cuboid = self._cuboid_to_set(instr.cuboid.x_range, instr.cuboid.y_range, instr.cuboid.z_range)
        
        if instr.on_or_off == "on":
            self._cuboid = self._cuboid | cuboid   # union
        else:
            self._cuboid = self._cuboid - cuboid   # diff
    
    def _cuboid_to_set(self, x_range: tuple, y_range: tuple, z_range: tuple) -> set:
        """ Creates a new set of 'on' points, given a set of 3 pairs of cuboid vertices. """
        temp_cuboid = set()
        
        x_lower, x_upper = x_range[0], x_range[1]
        y_lower, y_upper = y_range[0], y_range[1]
        z_lower, z_upper = z_range[0], z_range[1]
        
        if self._bound > 0:
            x_lower = max(x_lower, -self._bound)
            y_lower = max(y_lower, -self._bound)
            z_lower = max(z_lower, -self._bound)
            
            x_upper = min(x_upper, self._bound)
            y_upper = min(y_upper, self._bound)
            z_upper = min(z_upper, self._bound)

        for x in range(x_lower, x_upper+1):
            for y in range(y_lower, y_upper+1):
                for z in range(z_lower, z_upper+1):
                    temp_cuboid.add((x, y, z))
        
        return temp_cuboid
    
    def __repr__(self) -> str:
        return f"CuboidGrid:size={len(self._cuboid)}"

Things to note about this:

• Internally, it stores all on cubes as a set.
• Thus, the number of cubes turned on is given by the size of the set. We use the cubes_on property to return this value.
• It updates the number of on cubes in the reactor, by processing instructions, one instruction at a time.

• For each instruction:

  • We create a set that contains all the cubes described by the cuboid of this instruction.
  • We restrict the cubes in this set to be cubes that sit within the bounds, if we passed any. (Which, for Part 1, we did.)
  • If we’re turning cubes on, we simply union all the cubes in the instruction’s cuboid with the cubes that are already on.
  • Otherwise, we’re turning the cubes off, so subtract all the cubes in the instruction’s cuboid from teh cubes that are already on.

To run it, we first read in all the instructions and split them into lines:

input_file = os.path.join(SCRIPT_DIR, INPUT_FILE)
with open(input_file, mode="rt") as f:
    data = f.read().splitlines()

Then we convert each line into an Instruction object.

instructions: list[Instruction] = []
pattern = re.compile(r"(on|off) x=(-?\d+)..(-?\d+),y=(-?\d+)..(-?\d+),z=(-?\d+)..(-?\d+)")
for line in data:
    if (match := pattern.match(line)):
        instr, x_min, x_max, y_min, y_max, z_min, z_max = match.groups()
        reactor = Cuboid((int(x_min), int(x_max)), (int(y_min), int(y_max)), (int(z_min), int(z_max)))
        instructions.append(Instruction(instr, reactor))

This works by:

• Using regex to obtain capture groups that represent:
  • Whether on or off (instr)
  • The x start (x_min) and x end (x_max)
  • The y start (y_min) and y end (y_max)
  • The z start (z_min) and z end (z_max)
  • Note that each numeric capture group contains -? to allow for optional negative numbers.
• We create a Cuboid from the x, y, and z ranges.
• We add the Instruction to the list of instructions.

Finally, we create our Reactor object, with the required bounds, and then process each Instruction:

# Part 1 - Count how many cubes are on, with small bounds
logger.info("Part 1:")
reactor = Reactor(bound=50)
for instr in tqdm(instructions):
    reactor.update(instr)

logger.info("Using CuboidSet - cubes on: %d\n", reactor.cubes_on)

Here I’m using the very cool tqdm package. We use it by wrapping any iterable object. It returns an iterator that behaviours just like the original iterator, but you get a dynamically updating progress bar for free!

So that works, and it gives the right answer. Alas, it takes over 10 seconds, which doesn’t bode well for Part 2.

Part 2

Now we need to run the reboot steps for all cubes in the reactor, not just the ones within the +/-50 ranges.

The instructions tell us that with just the sample data, we end up with 2758514936282235 cubes turned on. That number is just too big to tackle with the same approach. Given that the same sample data only has 547648 on cubes for Part 1, even if my computer had enough RAM, and if the application scaled linearly, I’d still be waiting for many years before the program finishes. We’re going to need to be more clever.

My solution is to use coordinate compression. This is a technique where we take a large number of coordinates, and compress them down to fewer coordinates by eliminating all adjacent points where nothing interesting happens. As a really noddy example in one dimension:

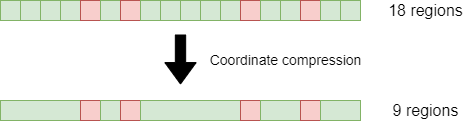
Here, we’ve taken 18 unit sized regions, which could be represented as x=0 through to x=17. We’ve then compressed the data, by ignoring any x values where nothing changes. This leaves us with only 9 regions that carry any useful information, i.e. where x is 0, 4, 5, 6, 7, 12, 13, 15, 16.

How might we apply this to our reactor problem? Well, let’s start by simplifying our reactor to one dimension. Here’s a simple 1D reactor example:

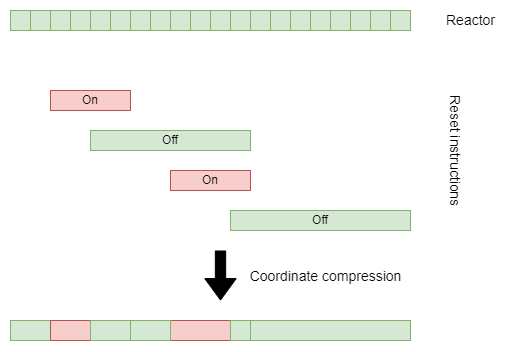
Note how we only mark coordinates where there are instructions that mark the beginning and end of a range. (In my code, I call these ranges intervals.)

How about a 2D example?

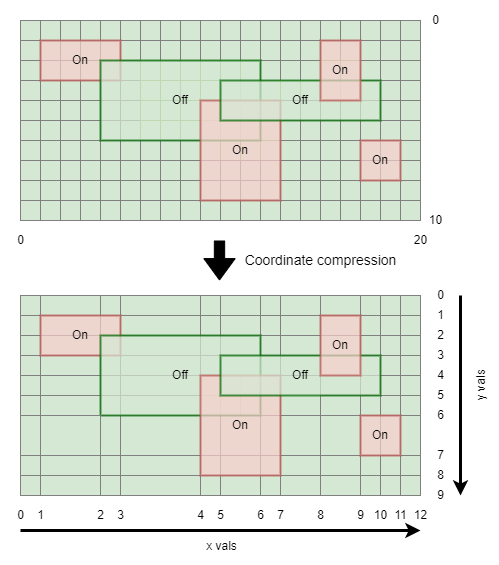
How does it work?

• Take all the x and y coordinates in the instructions, and assemble all the x values in ascending order, and all the y values in ascending order. These will be x and y values where something changes, i.e. either the start of an interval, or the end of an interval.
• The deltas between successive values in each list represent the size of all the intervals, in that particular dimension.
• Thus, by combining x, y coordinates and a matching pair of x and y segment lengths, we are able to obtain all the compressed regions.
• We then iterate through the instructions in instruction order.
  • For each instruction, determine the rectangle described by that instruction, in terms of its x start, x end and y start, y end coordinates.
  • For the pair of x values that correspond to the horizontal edges of the rectangle, map them back to index positions.
  • Now do the same for y values, i.e. corresponding to the vertical edges of the rectangle.
  • Now iterate through the x indexes from x1 index to x2 index, and for each, iterate through the y indexes from y1 index to y2 index.
    • Each loop gives us a segment that is part of an on or off rectangle.
    • So all we need to do is add in on segments, and remove off segments, as required.

Finally, let’s implement this for Part 2. I’ve created a class called CuboidDeterminator to do this:

class CuboidDeterminator():
    """ Represents number of points that are turned on in a 3D space. This class works using coordinate compression.
    Instructions are pre-processed to collapse to coordinates where something changes, i.e. the beginning or end of a cuboid.
    We obtain a sorted list of coordinates in each dimension, representing any interval boundaries in that dimension.
    For each boundary, we have an associated length of the corresponding cuboid 'segment'.
    Finally, we work out how many cubes there are in all the 'on' cuboid segments, and return the total. """
    
    def __init__(self, instructions: list[Instruction]) -> None:
        self._instructions = instructions

    def perform_reset(self) -> int:
        """ Process all the instructions, e.g. 
        on x=10..12,y=10..12,z=10..12, on x=11..13,y=11..13,z=11..13.
        Instruction order is not important.  We'll convert to an ordered list.
        
        Returns int: Total cubes turned on. """
        
        # Here we will store all cube positions where something interesting happens, i.e. a cuboid begins or ends
        x_vals = []
        y_vals = []
        z_vals = []
                
        # Get all the intervals, i.e. where an instruction changes something
        for instruction in self._instructions:
            cuboid = instruction.cuboid
            
            # Add the intervals (vertices) in this instruction
            x_vals.append(cuboid.x_range[0])
            x_vals.append(cuboid.x_range[1]+1)
            y_vals.append(cuboid.y_range[0])
            y_vals.append(cuboid.y_range[1]+1)
            z_vals.append(cuboid.z_range[0])
            z_vals.append(cuboid.z_range[1]+1)
    
        # All dimensions in numeric order
        x_vals.sort()
        y_vals.sort()
        z_vals.sort()
        
        # Store the intervals (ranges) between each successive value in a given dimension        
        x_intervals = [x_vals[i+1]-x_vals[i] for i in range(len(x_vals)-1)]
        y_intervals = [y_vals[i+1]-y_vals[i] for i in range(len(y_vals)-1)]
        z_intervals = [z_vals[i+1]-z_vals[i] for i in range(len(z_vals)-1)]
        
        on_indexes = set()
        
        # Now apply on and off instructions, i.e. add or remove cuboids in the right order
        for instruction in tqdm(self._instructions):
            # unpack the vertices of this cuboid
            x1, x2 = instruction.cuboid.x_range[0], instruction.cuboid.x_range[1]
            y1, y2 = instruction.cuboid.y_range[0], instruction.cuboid.y_range[1]
            z1, z2 = instruction.cuboid.z_range[0], instruction.cuboid.z_range[1]
            
            # Determine all the cuboid 'segments' we need to turn on.
            # A given cuboid in an instruction could contain many smaller cuboid 'segments'.
            # Get the indexes for the values given by each instruction, in a given dimension.
            # E.g. the first cuboid might give us x1 of 0 and x2 of 2. 
            # (Because x=1 might be the start of a different cuboid.)
            x1_index, x2_index = bisect_left(x_vals, x1), bisect_left(x_vals, (x2+1))
            y1_index, y2_index = bisect_left(y_vals, y1), bisect_left(y_vals, (y2+1))
            z1_index, z2_index = bisect_left(z_vals, z1), bisect_left(z_vals, (z2+1))
            
            for x_intv_index in range(x1_index, x2_index):
                for y_intv_index in range(y1_index, y2_index):
                    for z_intv_index in range(z1_index, z2_index):
                        # add starting coords corresponding to cuboid segments to turn on / off
                        if instruction.on_or_off == "on":
                            on_indexes.add((x_intv_index, y_intv_index, z_intv_index))
                        else:
                            # use discard, to remove cuboid segments that we have previously 'turned on'
                            # I.e. because an off instruction might overlap.  
                            # If it doesn't overlap, there will be nothing to discard.
                            on_indexes.discard((x_intv_index, y_intv_index, z_intv_index))
        
        logger.info("%d 'on' segments identified.", len(on_indexes))
        logger.info("Computing interval volumes. This might take a while...")
        
        total_cubes_on:int = 0

        # Each 'on' coord will align to a triplet of interval lengths, i.e. to give the volume of that cuboid 'segment'.
        # This gives us the size of the 'on cuboid', i.e. how many cubes are 'on' in the cuboid
        # Wrap our set with tqdm to provide a progress bar
        for x_intv_index, y_intv_index, z_intv_index in tqdm(on_indexes):
            len_x = x_intervals[x_intv_index]
            len_y = y_intervals[y_intv_index]
            len_z = z_intervals[z_intv_index]
            total_cubes_on += len_x * len_y * len_z
        
        return total_cubes_on

The use of bisect_left is worthy of a quick mention. Basically, I’m using this to determine the index position of coordinate values in our sorted list of x, y and z values. I’m using this rather than the more usual x_vals.index(x1), because the index() method searches for an item sequentally, from beginning to end; whereas the bisect_left() method performs a binary search. Performing a binary search is quicker for sorted data. Switching from index() to bisect_left() shaves about 20 seconds off my program’s overall execution time.

We run it like this:

# Part 2 - Count how many cubes are on, with no bounds
logger.info("Part 2:")
reactor = CuboidDeterminator(instructions)
logger.info("Using CuboidDeterminator - cubes on: %d", reactor.perform_reset())

And it follows exactly the same logic as described above, for the 2D example.

It works! Alas, it is a bit slow and takes over 3 minutes to run. So once again, I’m using tqdm to generate progress bars.

17:49:28.373:INFO:__main__:     Part 1:
100%|███████████████████████████████████████████████████████████████████| 420/420 [00:12<00:00, 33.14it/s]  
17:49:41.079:INFO:__main__:     Using CuboidSet - cubes on: 547648
17:49:41.080:INFO:__main__:     Part 2:
100%|███████████████████████████████████████████████████████████████████| 420/420 [02:01<00:00,  3.46it/s]  
17:51:42.414:INFO:__main__:     132571629 'on' segments identified.
17:51:42.416:INFO:__main__:     Computing interval volumes. This might take a while...
100%|██████████████████████████████████████████████████| 132571629/132571629 [01:14<00:00, 1790469.93it/s]  
17:53:31.546:INFO:__main__:     Using CuboidDeterminator - cubes on: 1206644425246111
17:53:31.547:INFO:__main__:     Execution time: 243.1747 seconds

That’s a flippin’ large number!

‹›