Advent of Code 2021 - Day 21

Day 21: Dirac Dice

Useful Links

‹›

Concepts and Packages Demonstrated

lru_cache itertools.product Abstract class ABC generator memoization

yieldrecursion

Problem Intro

Okay, we’re going to play a game of Dirac Dice. Part 1 was nice and easy. Part 2 nearly broke my brain.

So, we have two players (each with their own pawn), a single die, and a game board with a circular track. The track contains 10 spaces, marked 1 through 10.

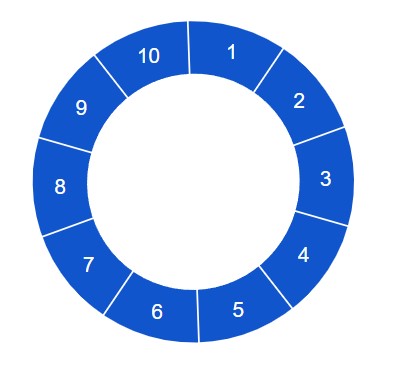
Diract Board

We’re told:

Players start with a score of 0.
Each player starts on a random space. The starting space does not contribute to the initial player score.
Players take turns. On a player’s turn, the player rolls the die 3 times.
The sum of the die rolls is the number of spaces they move, clockwise. Whatever space they land on, that is the score they are awarded for that turn. This is added to their existing score.

Part 1

We’re given a 100 sided deterministic die. I.e. every roll of the die returns an incrementing number from 1 to 100. When it gets to 100, we go back to 1. The game is won when a player reaches a score of at least 1000.

What is the product of the score of the losing player and the number of times the die was rolled in the game?

This is quite an easy problem, and we get to play with a few new things.

Setup

Some new things here, which we’ll cover as we get to them.

from abc import ABC, abstractmethod
from functools import lru_cache
import logging
import os
import time
from typing import Iterator, NamedTuple
from copy import deepcopy
from itertools import product

SCRIPT_DIR = os.path.dirname(__file__) 
INPUT_FILE = "input/input.txt"
# INPUT_FILE = "input/sample_input.txt"

logging.basicConfig(format="%(asctime)s.%(msecs)03d:%(levelname)s:%(name)s:\t%(message)s", 
                    datefmt='%H:%M:%S')
logger = logging.getLogger(__name__)
logger.setLevel(logging.DEBUG)

Solution

First, a class for the players:

class Player(NamedTuple):
    """ A player has a current position on the board, and a cumulative score """
    posn: int
    score: int

This subclasses NamedTuple. It’s a lot like the more powerful Dataclass. It allows us to create a class which is actually a tuple, but where the attributes of the tuple can be referenced by name.

Now we’ll create an abstract class, called AbstractDie:

class AbstractDie(ABC):
    """ Abstract die """
    def __init__(self, faces: int) -> None:
        self._faces = faces
        self._total_rolls = 0   # How many times have we rolled this die
        self._roll_gen = self._roll()   # A generator that performs the roll.
            
    @property
    def total_rolls(self):
        return self._total_rolls
    
    def roll(self):
        """ This is how we roll the die. Calls next() on the roll generator. """
        return next(self._roll_gen)
    
    @abstractmethod
    def _roll(self) -> Iterator[int]:
        """ We need to override this method. """
        return NotImplemented

The concept of an abstract class is that it provides some functionality that we can reuse in subclasses, but the abstract class itself cannot be instantiated. This is because the abstract class has one or more abstract methods, meaning that these methods do not yet have any actual implementation. So when we extend the abstract class, we need to provide an implementation for any abstract methods. In our AbstractDie, we can see that the _roll() method lacks any implementation, and is decorated as @abstractmethod.

Note that our AbstractDie class in inherits from ABC, i.e. the abstract base class. This is what marks our class as abstract.

If we try to do something like this:

die = AbstractDie(faces=100)

Then we’ll get an error like this:

TypeError: Can't instantiate abstract class AbstractDie with abstract method _roll

Other things to note about our AbstractDie:

We pass in the number of faces, when we construct the die.
It sets the instance variable _roll_gen to point to the _roll() method. It expects that method to be a generator. I.e. a form of iterator that returns a new object whenever the generator is passed to next().
Furthermore, we provide a public method roll(), which actually returns the next() item from our generator.

Now let’s implement our DeterministicDie:

class DeterministicDie(AbstractDie):
    """ Subclass of AbstractDie. Persists state between rolls.
    Always yields an incrementing int from the number of available faces, starting at 1.
    E.g. from 1-100. When we get to the number of faces, we wrap back around to 1. """
    
    def _roll(self) -> Iterator[int]:
        """ Yield the next available number. """
        while True:
            for i in range(1, self._faces+1):
                self._total_rolls += 1
                yield i

Nice and short. This is a subclass of AbstractDie, so we only need to override the abstract method, i.e. the _roll() method. This method yields incrementing values of i (i.e. from 1 to 100), and then wraps back around to 1, by virtue of being in an infinite while True loop. Note the use of the yield keyword here. It works like a return statement, but allows the method execution to continue on the very next method line, when we next call the method. E.g. if i has a value of 50 and we’ve just yielded that value, then when we next call roll(), which in turn calls next() on our _roll() method, then the method will continue within the for loop, setting i to 51.

Now let’s define a class for the Game itself:

class Game():
    """ We're on a circular track, with grid numbers 1 to 10. The player moves around the circle with each go.
    If the player lands on number x, the player gains x points.
    The player starts on an arbitrary grid number, and with a score of 0. """
    SPACES = 10
    ROLLS_PER_TURN = 3    
    
    def __init__(self, players: list[Player], die: AbstractDie, target: int) -> None:
        self._players = players  # Our two players.
        self._die = die          # Our die may be deterministic, so we need to store die state
        self._target = target    # The score a player needs to reach, to win the game    
    
    @property
    def players(self):
        return self._players
    
    @property
    def die(self):
        return self._die
    
    def play(self) -> int:
        """ Play a game. Each player takes a turn, until the target score is reached by a player. """
        while True:
            for player_num in range(len(self.players)):
                score = self._take_turn(player_num)
                if score >= self._target:   # This player has won!
                    return player_num
        
        assert False, "Game should end!"
        
    def _take_turn(self, player_num: int) -> int:
        """ Takes a turn for this player.  Roll the die n (e.g. 3) times, to give score x.
        Then move around the circle x places.  Whatever we land on, that's the score returned.
        Add this to existing score. Update the player.  Returns the cumulative score of the player """

        old_posn, old_total = self.players[player_num] # unpack the player
        
        die_score = sum(self._die.roll() for i in range(Game.ROLLS_PER_TURN)) # Roll n times
        new_posn = (((old_posn + die_score)-1) % Game.SPACES) + 1 # Move forward n spaces
        new_total = old_total + new_posn  # Add new board position to existing player score
        self.players[player_num] = Player(new_posn, new_total)  # Update the player
        
        return new_total

When we create a new Game, we pass in a list of players (there will be two), a die instance (which will be a subclass of AbstractDie), and the score we need to reach, for the game to end.

After initialisation, the game is played by calling play() on our Game instance.

We alternate between our two players, i.e. with the current player passed to _take_turn().
Taking a turn results in the player landing on a new space, which returns a new cumulative score.
If the score exceeds the target (i.e. 1000), then the game ends. The winning player number is returned.

The _take_turn() method:

Gets the current player position and score.
Performs our three die rolls, and then gets the sum of those rolls.
Determines the new position, by moving forward the number of spaces given the sum of the die rolls.
Updates the player’s score, based on that new position.

Finally, we run it:

    input_file = os.path.join(SCRIPT_DIR, INPUT_FILE)
    with open(input_file, mode="rt") as f:
        data = f.read().splitlines()

    init_players: list[Player] = []
    for line in data:
        tokens = line.split() # Into 5 tokens, e.g. "Player" "1" "starting" "position:" "4"
        init_players.append(Player(posn=int(tokens[-1]), score=0))
    
    # Part 1
    players = deepcopy(init_players)
    die = DeterministicDie(faces=100)
    game = Game(players, die, target=1000)
    won = game.play()
    
    total_rolls = game.die.total_rolls
    logger.info("Die has been rolled %d times", total_rolls)
    logger.info("Player %d won with score of: %d", won+1, players[won].score)
    logger.info("Part 1 result = %d\n", total_rolls * min(player.score for player in game.players))

This is what we’re doing here:

Start by parsing the input str to get starting positions. We create Player objects from these starting positions. We set their scores to 0.
We then create a 100-sided DeterministicDie.
We then create a new Game instance, passing in our players, the DeterministicDie, and the target score of 1000.
Finally, we run game.play().
We can get the total number of die rolls from game.die.total_rolls. I.e. die is a property of our Game class, and total_rolls is a property of our DeterministicDie.
We can get the score of the losing player, by getting the min() player.score of all the players in the game. (Of course, there are only two.)

So, Part 1 was pretty easy!

Part 2

Well, this escalated quickly!

We now only have a 3-sided die. It’s just as well. It’s a quantum die. Every roll of the die splits the universe into three different universes: one for each of the possible roll outcomes!

To win, we only need to reach a score of 21.

Our objective:

Find the player that wins in more universes; in how many universes does that player win?

OMG.

Let’s consider Player 1’s first turn. On the first roll, we generate 3 universes, with roll values of 1, 2 and 3. On roll 2, each of those universes splits into 3 more universes. And on roll 3, each of those universes splits into 3 more universes!! Thus, 3 rolls gives us 3³ = 27 different universes per turn:

Roll 1                1                 2                 3
Roll 2          1     2     3     1     2     3     1     2     3
Roll 3        1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3

Sum           3 4 5 4 5 6 5 6 7 4 5 6 5 6 7 6 7 8 5 6 7 6 7 8 7 8 9

To determine the 27 different different sums that are achievable from our 3 rolls programmatically, we can use a cartesian product:

TRIPLE_ROLL_SUMS = [sum(score) for score in product(range(1, 4), repeat=3)] 

range(1, 4) generates the numbers 1, 2, and 3. It is equivalent to [1, 2, 3].

Then we use another handy utility from the itertools package. This is asking for the cartesian product of [1, 2, 3][1, 2, 3][1, 2, 3]. The range is repeated three times, because of the repeat argument. The product function returns all the valid combinations of the values of these three ranges, and returns all these combinations as tuples. It’s a shorthand for doing a nested for loop 3 times.

So:

product(range(1, 4), repeat=3)

Gives us these tuples:

(1, 1, 1)
(1, 1, 2)
(1, 1, 3)
(1, 2, 1)
(1, 2, 2)
(1, 2, 3)

And so on.

And when we sum() each tuple in the list comprehension, the result is:

[3, 4, 5, 4, 5, 6, 5, 6, 7, 4, 5, 6, 5, 6, 7, 6, 7, 8, 5, 6, 7, 6, 7, 8, 7, 8, 9]

Great. Those are the different 3-roll die sums for the 27 different universes of the first move of the game. If player 2 now takes their turn, they have 27 different universes that follow each of the universes created by player 1. Thus, with two turns, we have 27*27 = 729 universes. After three turns, there are nearly 20000 universes. After four turns, half a million universes. After 5 turns, 14 million universes. You can see that this is going to get rapidly out of hand.

In theory, if both players were only ever rolling a score of 1 with their die, you could envisage a game that takes 14 turns to finish (i.e. 7 turns each, with each turn having a cumulative roll score of 3). That would result in 109418989131512359209 universes. Way too many to process!

So, what’s our game plan?

Clearly we can’t simulate every possible universe. The solution space is just too large. But it turns out there aren’t that many different game states. And from any given game state, we just need to work out how many ways there are to win from that state. But what is a game state?

A game state is represented by:

The position of the player on the board; there are only 10 different positions (1 through 10) per player.
The score of the player; there are only 21 different scores (0 through 20, since any larger score results in the game ending) per player.

Thus, we have 10*10*21*21 = 44100 game states. That means only 44100 unique universes from which a player can win. Clearly, there are a lot more possible universes than that. But it doesn’t matter, since we can cache game states we’ve seen before, and whenever we see a previous game state, we know exactly how many ways there are to win from that game state.

So now we can solve using recursion. Recall from Day 14 that to implement recursion, we need:

A base case, where the function simply returns a value.
Any other cases, where the function calls itself, and where each call moves closer to the base case.

We’ll create a function that determines how many ways each player can win from the current game state. This is called count_wins().

So what’s our base case? This is the case where we’ve reached our goal, and the function should exit. We’ve reached our goal when either player has won. Either player has won when their score is >= 21. So if Player A has >= 21, then there is 1 way that Player A can win, and 0 ways that Player B can win. (Since Player A has won.) And if Player B has >= 21, there is 1 way that Player B can win, and 0 ways that Plaer A can win.

In all other cases, we want to determine our 27 different triple roll outcomes possible for this player, move the player the appropriate number of spaces, and update the player’s score; thus creating a new game state. Then we recurse into our function with this new game state. But crucially, when we recurse, we swap the player A and player B positions as parameters to the function call, since if Player A took the last turn, then Player B needs to take this turn.

@lru_cache(maxsize=None)    
def count_wins(posn_a: int, posn_b: int, score_a: int, score_b: int) -> tuple[int, int]:
    """ Return number of universes in which each player can win from this state.
    With a given game state, player a starts at posn_a with score_a and player b at posn_b with score_b.
    Player a's turn.

    Returns:
        tuple[int, int]: (Ways to win for player a, ways to win for player b)
    """
    if score_a >= 21:
        return (1, 0)   # Player A has won; player B has lost. No other options are possible.
    
    if score_b >= 21:
        return (0, 1)   # Player B has won; player A has lost. No other options are possible.
    
    wins_a = wins_b = 0  # Initialise; no wins yet
    
    # Perform the triple roll to get a new game state, and then handover to other player to take their turn
    for score in TRIPLE_ROLL_SUMS:  # 27 differnet recursions for this turn
        new_posn_a = (posn_a + score - 1) % Game.SPACES + 1     # move player
        new_score_a = score_a + new_posn_a                      # update player score
        
        # Now recurse. Next move is from player b. So, next call will return (ways b, ways a).
        wins_b_from_here, wins_a_from_here = count_wins(posn_b, new_posn_a, score_b, new_score_a)
        wins_a += wins_a_from_here
        wins_b += wins_b_from_here
        
    return wins_a, wins_b

The last point to note is the addition of the decorator @lru_cache(). This implements a least recently used cache, such that when the function is given a set of parameters that have been used before (i.e. a previously seen game state), then the function returns the same result as it did before, without actually doing any work. Thus, the function is caching previously seen states, including all the recursions that a given state would have needed to process. We pass maxsize=None to the @lru_cache() decorator, such that there’s no limit on the number of parameter permutations that are cached.

This combination of recursion, combined with caching the results of a call we’ve seen before, is called memoization.

We call the code, as follows:

   # Part 2
    # With a given game state, player_1 starts at posn_1 with score_1and player_2 at posn_2 with score_2.
    # How many ways can they win from this state?
    players = deepcopy(init_players)
    wins = count_wins(players[0].posn, players[1].posn, players[0].score, players[1].score)
    for i, win in enumerate(wins):
        logger.info("Player %d wins: %d", i+1, win)
        
    logger.info("Part 2: universes in which the player wins the most = %d", max(wins))

And the output looks like this:

57:08.588:INFO:__main__:     Die has been rolled 861 times
57:08.590:INFO:__main__:     Player 1 won with score of: 1008
57:08.590:INFO:__main__:     Part 1 result = 684495

57:08.799:INFO:__main__:     Player 1 wins: 138289532619163
57:08.799:INFO:__main__:     Player 2 wins: 152587196649184
57:08.799:INFO:__main__:     Part 2: universes in which the player wins the most = 152587196649184    
57:08.799:INFO:__main__:     Execution time: 0.2135 seconds

Wow, that’s a lot of universes!

‹›