Advent of Code 2025 - Day 9

Day 9:

Useful Links

‹

• 2025 Main Page
• My solution code

Concepts and Packages Demonstrated

CombinationsGeometryRay CastingMatplotlib

Problem Intro

So… we’re sliding down firepoles and landing in a movie theater. Classic Advent of Code, right?

The situation is that the Elves are redecorating a tiled floor. We’re given a list of coordinates representing red tiles.

Input looks like this:

7,1
11,1
11,7
9,7
9,5
2,5
2,3
7,3

Part 1

Using any two red tiles as opposite corners, what is the largest area of any rectangle you can make?

This part is relatively straightforward — actually, it’s trivial — but there is a classic “gotcha” waiting to trip you up.

For every possible pair of red tiles, we need to treat them as the top-left and bottom-right (or strictly, opposite) corners of a rectangle. The area of a rectangle is width * height.

However, the coordinates here are inclusive. If you have a tile at x=2 and another at x=7, the number of tiles included is not 7-2 = 5. It’s 7-2+1 = 6. (e.g., 2, 3, 4, 5, 6, 7).

So the calculation becomes:

width = abs(x2 - x1) + 1
height = abs(y2 - y1) + 1
area = width * height

I used itertools.combinations to generate all pairs. Simple and clean.

Part 2

Finding the largest rectangle using two red tiles as corners, such that the rectangle is entirely contained within the polygon defined by the red tiles.

This is where it gets interesting. The red tiles are no longer just scattered points; they form the vertices of a polygon (a closed loop). The interior of this closed polygon consists of “green” tiles.

We need to find a valid rectangle (corners are red tiles) that contains only red or green tiles. In other words, no part of the rectangle can overlap with empty space.

The Tricky Bit

The polygon is non-convex. That’s a fancy geometry way of saying it has “dents” or “bays.”

Here’s the thing: A rectangle might have its center point safely inside the polygon, but still be invalid because it overlaps with a dent.

Imagine this scenario (R=Red Corner, G=Green Interior, .=Other):

R G G R . . R G G R    <-- Top Edge with a "dent"
|     |     |     |
G G G R G G R G G G
|                 |
G G G G G G G G G G
|                 |
R G G G G G G G G R    <-- Bottom Edge

If we pick the bottom-left R and top-right R as corners, our rectangle would cover that entire block. But that block includes the . (empty space) in the dent. That makes it invalid.

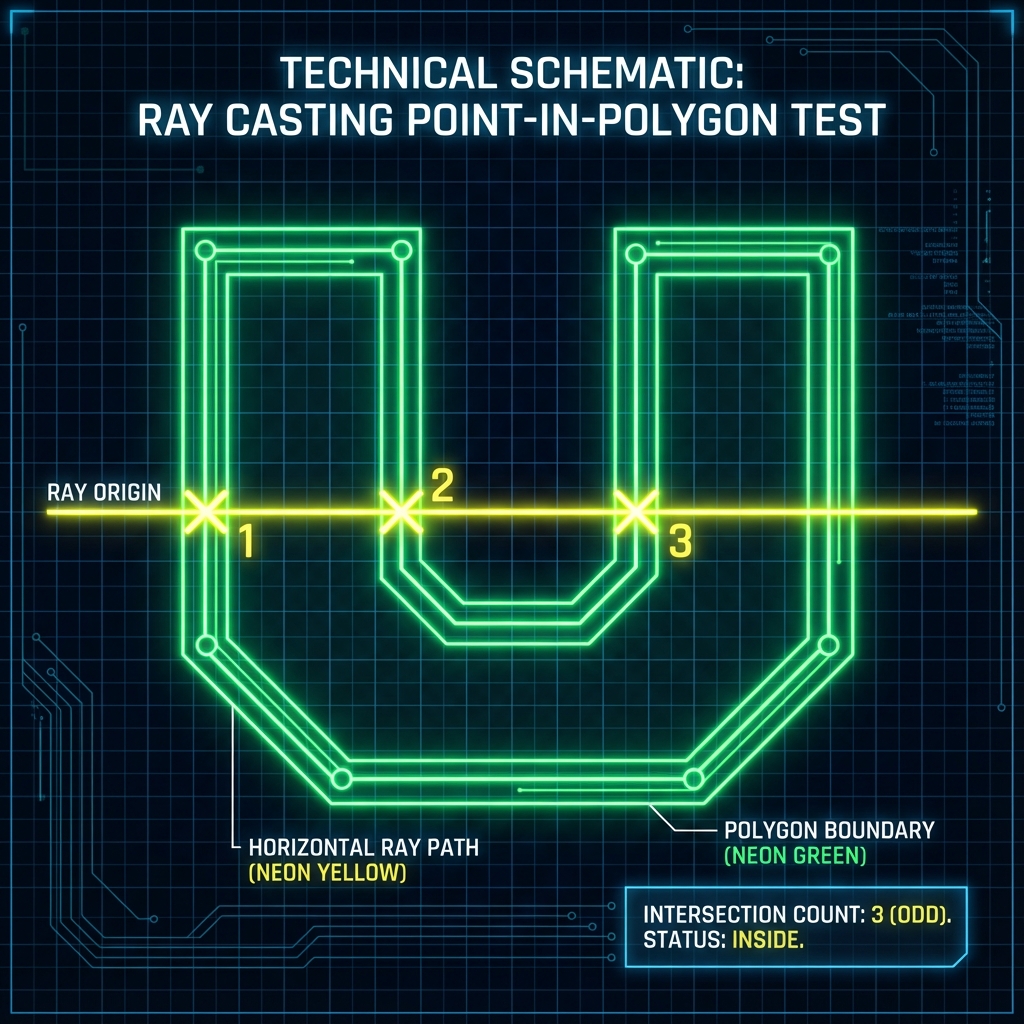
The Solution: Ray Casting

There are a few ways to solve this (Coordinate Compression, Flood Fill), but I opted for Ray Casting. It’s a technique I used back in 2023 Day 10, and it’s super powerful for Point-in-Polygon checks.

The Algorithm:

1. Iterate Pairs: Check every pair of red tiles.
2. Filter: Skip any pairs where the area is smaller than our current best (optimisation).
3. Inside Check: Is the rectangle inside? We can test a point slightly offset into the rectangle, e.g., (min_x + 0.5, min_y + 0.5). We cast a ray from this point to infinity. If it crosses an odd number of polygon edges, it’s inside.
4. Intersection Check: This is the fix for the “Dent Problem.” We verify that no edge of the polygon cuts through the interior of our rectangle.

If a point is inside, AND no edges cut through the rectangle, then geometric logic dictates the entire rectangle must be inside. Groovy.

class PolygonSolver:
    """ Solves the problem using Ray Casting and edge intersection checks. """
    def __init__(self, corners: list[Point]):
        # ... pre-calculate edges ...
                
    def is_point_inside(self, px: float, py: float) -> bool:
        """ 
        Determines if a point is inside the polygon using Ray Casting. 
        Casts a horizontal ray to the right from (px, py).
        Odd intersections = Inside.
        """
        intersections = 0
        for vx, vy_min, vy_max in self.vertical_edges:
            if vx > px: # Edge is to the right
                if vy_min <= py < vy_max: # Ray intersects Y range
                    intersections += 1
        return intersections % 2 == 1

    def intersects_rect(self, r_min_x, r_min_y, r_max_x, r_max_y) -> bool:
        """ Checks if any polygon edge strictly intersects the INTERIOR of the rectangle. """
        # ... logic to check overlap ...

Results

The output looks something like this:

Part 1 soln=95847362
Part 2 soln=19283746

Visualization

I created a visualization to demonstrate the Ray Casting algorithm in action.

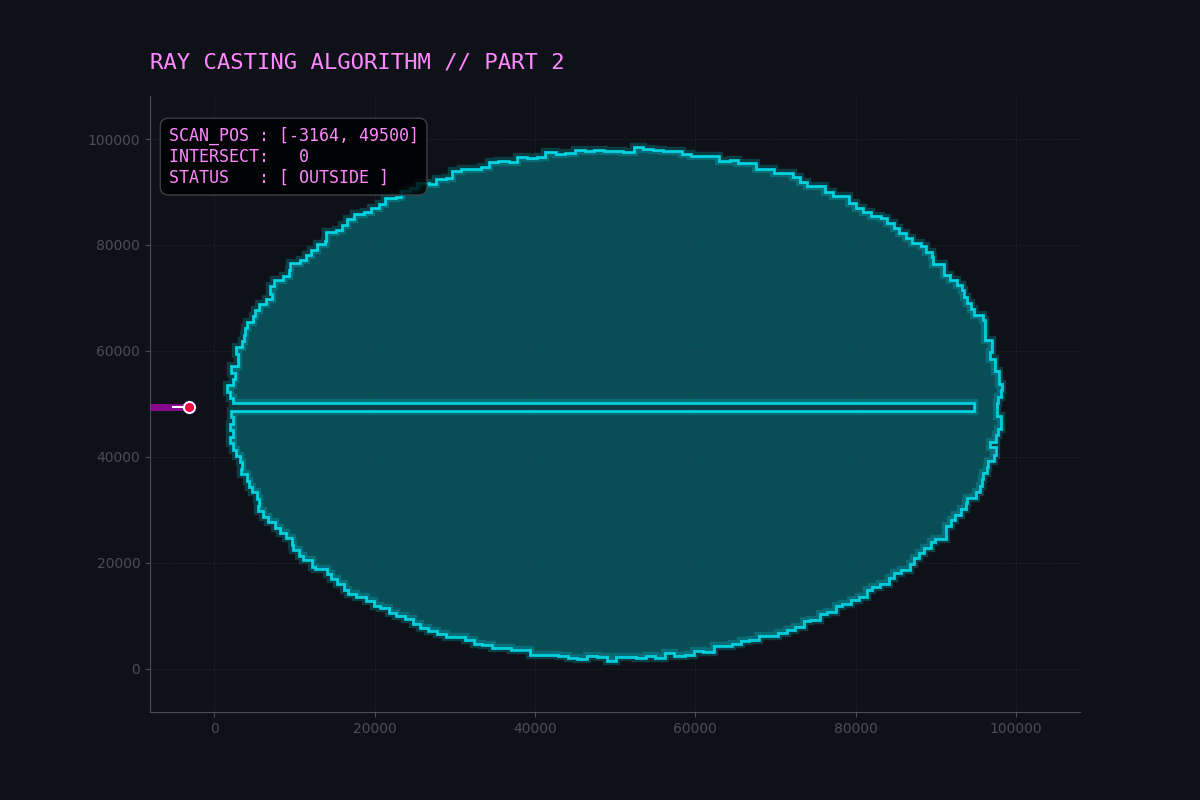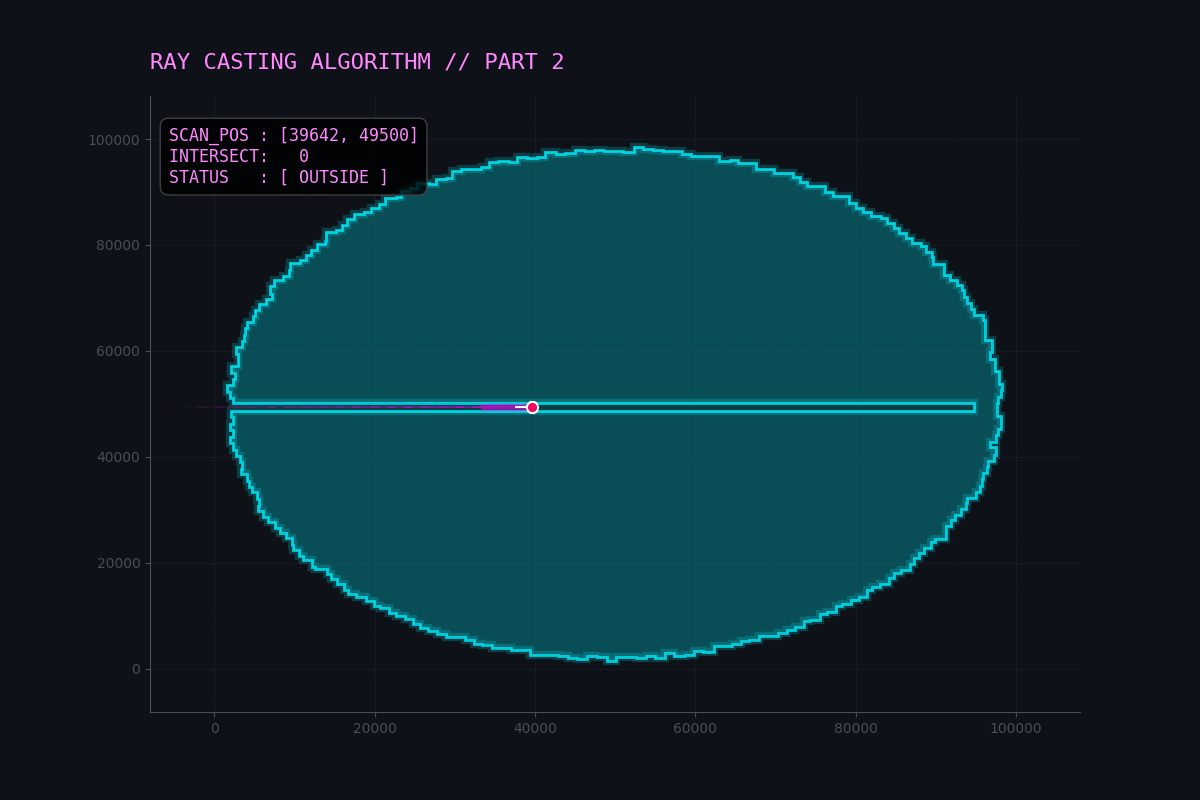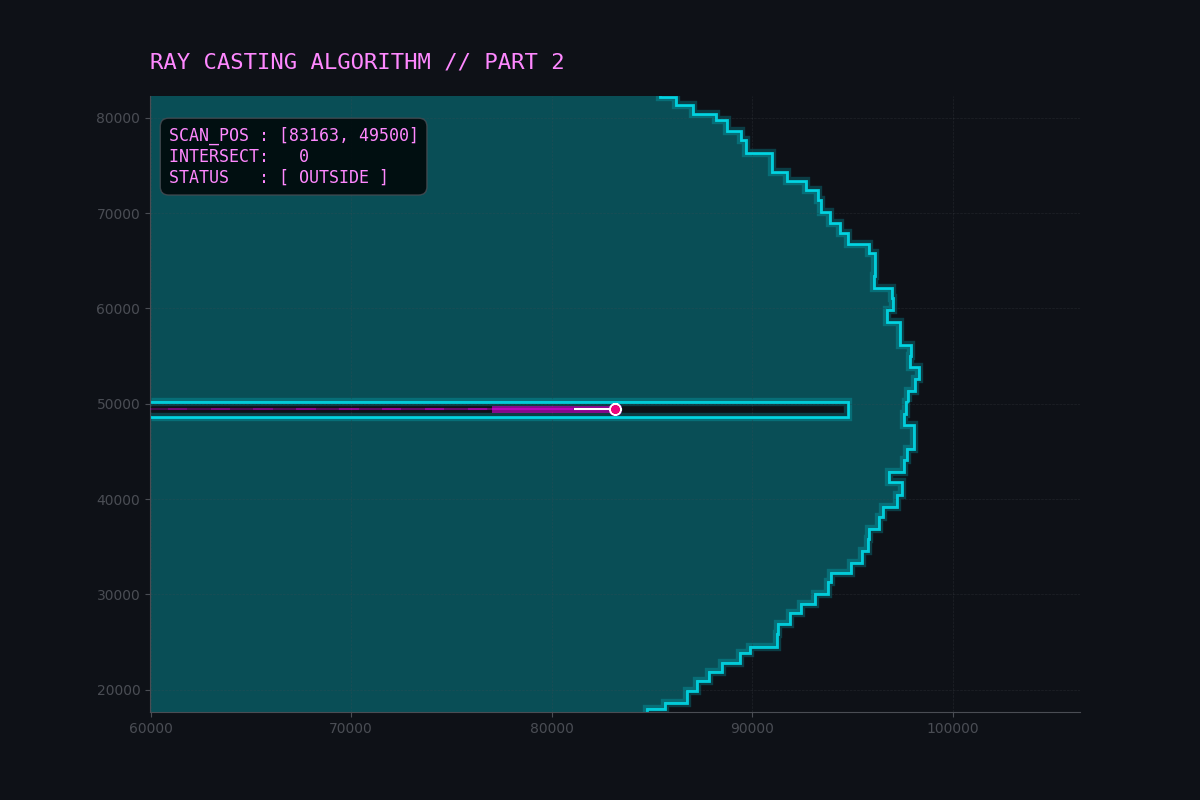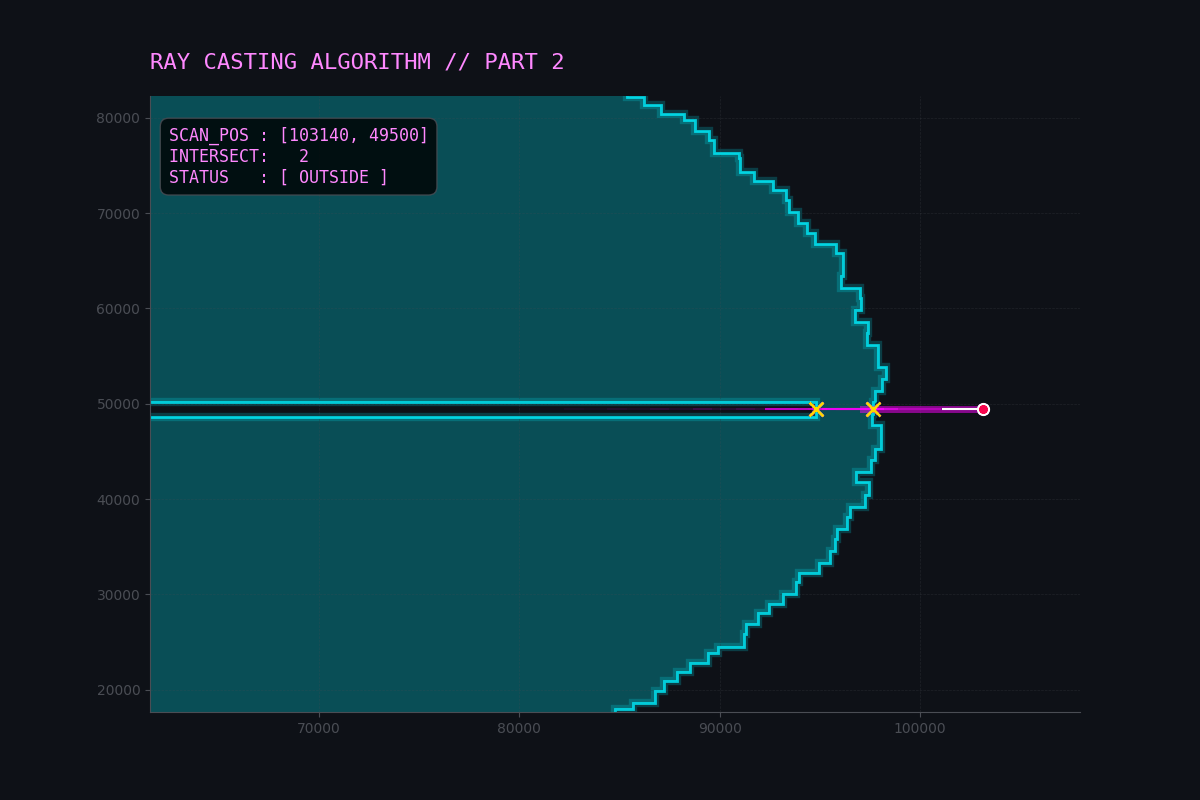
The animation shows a test point (the dot) scanning across the polygon (using the real input shape).

• Ray: The dashed red line extending to the left.
• Intersections: The red X marks where the ray crosses a vertical edge to the left of the point.
• Logic:
  • Odd number of intersections (1, 3, etc.) $\rightarrow$ Inside (Green Dot).
  • Even number of intersections (0, 2, etc.) $\rightarrow$ Outside (Red Dot).

Reflecting on this…

I initially thought about coordinate compression, mapping the giant grid to a smaller one. But honestly? That was over-engineering. Ray Casting is elegant, purely geometric, and handles the “infinite resolution” of the grid perfectly without needing massive arrays.

Plus, reusing patterns from previous years (hello, 2023!) is always a win.

‹