Advent of Code 2021 - Day 18

Day 18: Snailfish

Useful Links

‹›

• 2021 Main Page
• My solution code

Concepts and Packages Demonstrated

Regular expressionsreducepermutations

mathliteral_evaldequerecursionstaticmethodbinary treeDepth-First Search (DFS)

Problem Intro

There are some people in the world - out of the roughly 200,000 that took part in the 2021 AoC - that managed to complete the solutions to this challenge in under 30 minutes!

I’m not one of those people. This was tricky, and it took me hours!

I created two solutions to this problem:

• Solution #1 - Converting to a str and then doing lots of str manipulation
• Solution #2 - By building a binary tree, and then navigating the tree using depth-first search

So, we need to help a snailfish with its math homework. Snailfish math is pretty darn weird. The input looks like this:

[[[0,[5,8]],[[1,7],[9,6]]],[[4,[1,2]],[[1,4],2]]]
[[[5,[2,8]],4],[5,[[9,9],0]]]
[6,[[[6,2],[5,6]],[[7,6],[4,7]]]]
[[[6,[0,7]],[0,9]],[4,[9,[9,0]]]]
[[[7,[6,4]],[3,[1,3]]],[[[5,5],1],9]]
[[6,[[7,3],[3,2]]],[[[3,8],[5,7]],4]]
[[[[5,4],[7,7]],8],[[8,3],8]]
[[9,3],[[9,9],[6,[4,9]]]]
[[2,[[7,7],7]],[[5,8],[[9,3],[0,2]]]]
[[[[5,2],5],[8,[3,7]]],[[5,[7,5]],[4,4]]]

• Each line is a snailfish number.
  • Every snailfish number is a pair.
  • A pair is an ordered list of two elements.
  • An element is either another pair, or a regular number.
• Snailfish numbers can be added together. This is effectively the concatenation of two lists, followed by reduction.
• Snailfish reduction is the repetition of the first available step on this list, until no more reduction can be done.
  1. Exploding of any pairs nested inside four pairs.
     • Exploding removes an inner bracket and adds the inner numbers to either side.
     • It has the effect of reducing the overall list depth by 1.
  2. Splitting of any regular number that is 10 or greater, into a pair.
     • Essentially, it splits an int into a pair (x,y) of two integer halves.
     • It creates a new bracketed pair (x,y) from a regular number, one level deeper than the original number.

Note how each snailfish number has the exact same structure as a Python (nested) list. This will come in handy!!

The thing which caught me out for a while is that I hadn’t fully understood the explode instructions. In particular:

• Add the left number in the pair to the nearest left number (if there is one)
• Add the right number in the pair to the nearest right number (if there is one)
• AND replace the original pair with 0.

Part 1

We have to add all the snailfish numbers in our input, and then determine the magnitude of the resulting number?

We’re told that:

• The magnitude of a pair is 3 times the magnitude of its left element plus 2 times the magnitude of its right element.
• The magnitude of a regular number is just that number.

Solution 1

This solution takes our list and converts it to a str in order to check if it can be exploded or split, and to enable us to modify the str according to the rules.

Setup

from __future__ import annotations
import logging
from pathlib import Path
import time
import re
from functools import reduce
from math import ceil, floor
from itertools import permutations
from ast import literal_eval

SCRIPT_DIR = Path(__file__).parent
INPUT_FILE = Path(SCRIPT_DIR, "input/input.txt")
# INPUT_FILE = Path(SCRIPT_DIR, "input/sample_input.txt")

logging.basicConfig(format="%(asctime)s.%(msecs)03d:%(levelname)s:%(name)s:\t%(message)s", 
                    datefmt='%H:%M:%S')
logger = logging.getLogger(__name__)
logger.setLevel(logging.INFO)

The only new imports here are:

• ceil and floor from math
• literal_eval from ast

We’ll talk about those when we get to them.

Solution

First, we read in the data:

with open(INPUT_FILE, mode="rt") as f:
    # Each input line is a nested list. Use literal_eval to convert to Python lists.
    data = [FishNumber(literal_eval(line)) for line in f.read().splitlines()]

• We read in each line. Each line is a single snailfish number.
• Because each snailfish number is represented exactly like a Python list, it is a trivial matter to read the input data and store it as a list. We can use literal_eval() to do this. This function evaluates any string data that exists in a Python data structure format, and then stores it in that data structure. E.g. if you give literal_eval() a string in dict format, then the function returns a dict; if you give it string in list format, then it returns a list. The literal_eval() function is considered a safe way to evaluate an input string, since it will only evaluate a limited subset of data, i.e. data that conforms to a standard Python data type. There is a more dangerous function called eval(), which will take any input string and convert it to Python code. This is potentially a dangerous thing to do… So don’t do it!
• Having converted the input data to a list, we then use this list to construct a FishNumber.

Now for the FishNumber class:

class FishNumber():
    """ FishNumber stores a snailfish number internally. This class knows how to:
    - Add two FishNumbers to create a new FishNumber. 
    - Reduce snailfish numbers according to rules. """
    
    EXPLODE_BRACKETS = 4
    SPLIT_MIN = 10
    
    def __init__(self, fish_list: list) -> None:
        self._number = fish_list # internal representation as a list
         
    @property
    def number(self):
        return self._number
   
    def add(self, other: FishNumber) -> FishNumber:
        """ Creates a new FishNumber by concatenating two FishNumbers.
        Effectively, this is list extension. """
        return FishNumber([self.number] + [other.number])
        
    def reduce(self):
        """ Performs 'reduction' logic. I.e. explode and split, as required. """
        while True:
            if self._can_explode():
                self._number = self._explode()
            elif self._can_split():
                self._number = self._split()
            else:
                break

    def __repr__(self) -> str:
        return str(self.number)

Things to say about this class:

• The __init__() takes the input list and stores it as _number.
• The add() method simply concatenates two lists: this _number and the _number of another FishNumber instance.
• The reduce() method simply follows the rules, i.e.
  • Explode if we can.
  • Else split if we can.
  • Else quit the loop.

Now let’s add the FishNumber methods that do the hard work. First, exploding…

    def _can_explode(self) -> bool:
        """ Checks if we can explode by counting brackets. """
        str_repr = str(self._number)
        depth_count = 0
        for char in str_repr:
            if char == "[":
                depth_count += 1
                
            if char == "]":
                depth_count -= 1
                
            if depth_count > FishNumber.EXPLODE_BRACKETS:
                return True
        
        return False

    def _explode(self) -> list:
        """ Explodes the current list.
        Looks for first opening bracket that is sufficiently nested. Takes the pair of digits within.  
        Adds LH to first digit on the left. (If there is one.)
        Adds RH to the first digit on the right. (If there is one.)
        Then replaces the entire bracket with 0. """
        
        str_repr = str(self._number)    # convert list to str
        
        depth_count = 0
        for i, char in enumerate(str_repr):
            if char == "[":
                depth_count += 1
                
            if char == "]":
                depth_count -= 1
                
            if depth_count > FishNumber.EXPLODE_BRACKETS:
                assert str_repr[i+1].isdigit(), "Should have been a digit here"
                left_bracket_posn = i
                comma_posn = i+1 + str_repr[i+1:].find(",")
                right_bracket_posn = comma_posn + str_repr[comma_posn:].find("]")
                
                left_num = int(str_repr[i+1: comma_posn])
                right_num = int(str_repr[comma_posn+1:right_bracket_posn])
                
                # process left of pair
                # This regex looks for the first matching digits at the end
                if match := re.match(r".*\D+(\d+).*$", str_repr[:left_bracket_posn]):
                    # match first group, i.e. (\d+)
                    num_start, num_end = match.span(1)[0], match.span(1)[1]
                    new_num = int(str_repr[num_start:num_end]) + left_num
                    
                    # We might be inserting a bigger number
                    l_increase = len(str(new_num)) - (num_end-num_start)            
                    str_repr = str_repr[:num_start] + str(new_num) + str_repr[num_end:]
                    
                    left_bracket_posn += l_increase
                    comma_posn += l_increase
                    right_bracket_posn += l_increase
                    
                # process right of pair
                if match := re.search(r"\d+", str_repr[right_bracket_posn:]):
                    # match whole group
                    num_start = right_bracket_posn + match.span(0)[0]
                    num_end = right_bracket_posn + match.span(0)[1]
                    new_num = int(str_repr[num_start:num_end]) + right_num
                    str_repr = str_repr[:num_start] + str(new_num) + str_repr[num_end:]
                
                # replace the original pair with 0
                str_repr = str_repr[:left_bracket_posn] + "0" + str_repr[right_bracket_posn+1:]
                
                break
        
        new_num = literal_eval(str_repr)    # convert back to list
        return new_num

• To check if we _can_explode():
  • Count opening brackets. Every time we see an opener, add 1 to the count. Every time we see a closer, subtract 1.
  • If the count exceeds 4, then we’re sufficiently nested that we need to explode.
• To _explode():
  • Convert the entire _number to a str. We’ll then use some regex and string manipulation to the hard work.
  • Count brackets, as before. If we reach a nested pair that needs to be exploded:
    • Extract the int values of the left and right digits from this pair.
    • Now we look for digit to expand to on the left.
      • Use regex to find the last digit that is present before the opening bracket of our pair. This is done using the regex pattern ".*\D+(\d+).*$". It works by looking for digits \d+ to the right of a non-digit \D+ (such as [ or ,), to the left of any intervening characters.
      • If we find such a digit on the left, then convert it to an int, and add it to our left digit.
      • We have to mindful that the resulting digit might have a longer str reprentation, and we’d need to shift all our str indexes accordingly. E.g. 9 has a str length of 1, but 10 has a str length of 2.
    • Now look for a digit to expand to on the right. It’s basically the same as the left, but a bit simpler. E.g. the regex pattern is simply "\d+", meaning: find the first match of one or more digits.
  • Now replace the original pair (and including its brackets) with 0.
  • Finally, because we’ve been working with a str throughout, we need to convert it back to a list, so we once again use literal_eval().

Next, splitting…

    def _can_split(self) -> bool:
        """ We can split if there is a number >= 10 """
        str_repr = str(self._number)
        if re.search(r"(\d{2,})", str_repr):
            return True
        
        return False
        
    def _split(self) -> list:
        """ Split our fish number by taking the first n >= 10,
        and replacing with [floor(n/2), ceil(n/2)] """
        str_repr = str(self._number)
        if match := re.search(r"(\d{2,})", str_repr):
            num = int(match.groups()[0])
        
            if (num >= FishNumber.SPLIT_MIN):
                new_left_num = floor(num/2)
                new_right_num = ceil(num/2)
                new_str = "[" + str(new_left_num) + ", " + str(new_right_num) + "]"
                str_repr = re.sub(r"(\d{2,})", new_str, str_repr, count=1)

            new_num = literal_eval(str_repr)     # convert back to list
            return new_num
        
        assert False, "We should never get here since we're checking if we can split"
        return []

• To check if we _can_split(), just do a regex match against "(\d{2,})". This looks for any match of 2 or more digits. (Since we need to split any digit that is 10 or more.)
• To split():
  • Get a str representation of our _number list.
  • Find the location of our 2 consecutive digits. This number will be split in two.
  • Set the left number to the math.floor() of the number divided by 2. The floor() function rounds down.
  • Set the right number to the math.ceil() of the number divided by 2. The ceil() function rounds up.
  • Construct our new pair as a str, including its brackets and use re.sub() to substitude the original str for our new pair.
• Finally, convert back to a list and return.

The last thing we need to add to our FishNumber class is a way to determine its magnitude:

    @staticmethod
    def magnitude(fish_num) -> int:
        """ Magnitude is given by 3*LHS + 2*RHS for any pair of values. 
        If the values are themselves lists, we must recurse.
        If the values are themselves ints, we return the int value. 
        If the value is not part of a pair, simply return the value. """
        mag = 0
        
        # First check if this is a pair (list)
        if isinstance(fish_num, list):
            mag = 3*FishNumber.magnitude(fish_num[0]) + 2*FishNumber.magnitude(fish_num[1])
        elif isinstance(fish_num, int): # must be a single value
            mag = fish_num
    
        return mag

Since every snailfish number is a pair, we need to determine the magnitude of that pair. Since each element in the pair can be another pair, we know that recursion is going to be a good way to get the magnitude.

Thus, this method works by checking if the input parameter is itself an int, or a list. If it’s an int, we just return that value. If it’s a list, we know it represents a pair, so we need to return 3*left + 2*right. And we recurse to get the values of left and right.

Now let’s run it:

# Part 1
result = reduce(fish_add, data)  # Reduce to add n to n+1, then the sum to n+2, etc
logger.info("Result = %s", result)
mag = FishNumber.magnitude(result.number)
logger.info("Part 1 magnitude = %d", mag)

Just to avoid any potential confusion: in this code snippet, I’m using functools.reduce(), not FishNumber.reduce(). We’ve come across functools.reduce() before. It applies the specified function (the first parameter) to the first two items in the iterable (the second parameter). This generates a result, and it applies the function to this result and the third parameter. And then to the result of that and the fourth parameter. And so on.

In this way, we can use functools.reduce() to perform the fish_add() method against every number in the data supplied.

The fish_add() method looks like this:

def fish_add(left: FishNumber, right: FishNumber) -> FishNumber:
    """ Create new FishNumber by concatenating left and right.
    Then reduce the resulting number and return it """
    new_fish_num = left.add(right)
    new_fish_num.reduce()
    return new_fish_num  

This just uses the add() method from our FishNumber class, and then uses the FishNumber’s reduce() method on the resulting FishNumber.

Part 2

What is the largest magnitude you can get from adding only two of the snailfish numbers?

Very little additional code required here, since we’ve done all the hard work.

# Part 2
mags = []
for perm in permutations(data, 2): # All permutations of 2 fish numbers
    result = fish_add(perm[0], perm[1])
    mags.append(FishNumber.magnitude(result.number))
    
logger.info("Part 2: max magnitude = %d", max(mags))  

We use itertools.permutations() to get all permutations of two of the fish numbers, given the list of all the fish nubmers. Note that unlike itertools.combinations(), permutations considers order. I.e. a,b is different to b,a. Then add each pair of fish numbers, and determine the one with the largest magnitude.

Phew, that part was easy!

The final output looks like this:

21:34:16.431:INFO:__main__:     Result = [[[[7, 7], [7, 7]], [[7, 8], [0, 8]]], [[[8, 9], [9, 9]], [7, 7]]]
21:34:16.432:INFO:__main__:     Part 1 magnitude = 3869
21:34:45.502:INFO:__main__:     Part 2: max magnitude = 4671
21:34:45.504:INFO:__main__:     Execution time: 15.5432 seconds

Yay, it works! But it was a little slow. All that converting between list and str takes its toll. And all that str manipulation is quite slow.

We can do better!

Solution 2

This solution doesn’t do any manipulation as strings. Inatead, we create a binary tree from the list.

A tree is defined as a finite set of nodes, made up of a single root node, and one or more child nodes that are themselves leaf nodes, or are themselves trees. A binary tree is a special type of tree where:

• One node is the root node.
• Every child node has 0, 1 or 2 child nodes.
• If a node has no children, it is referred to as a leaf node.
• Every child node has exactly one parent node, and the child node is itself a left subtree, or a right subtree.

Thus, a binary tree looks something like this:

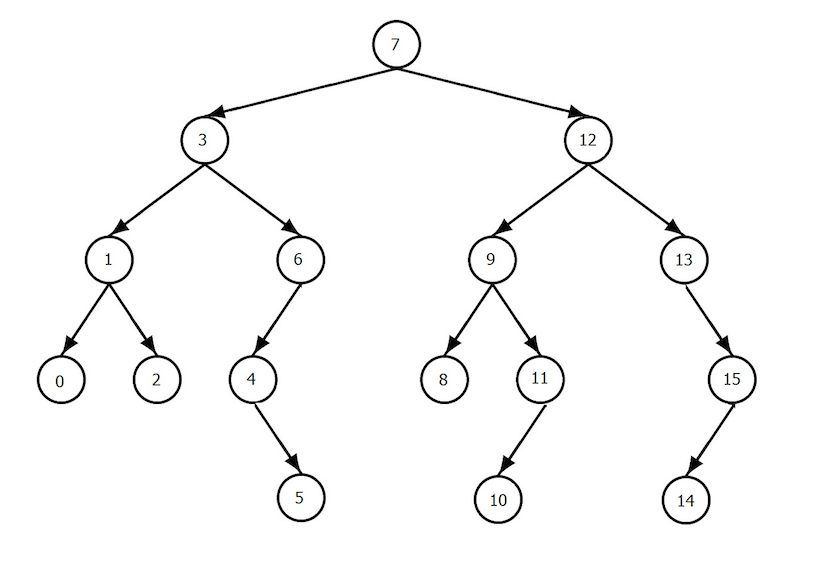
Our FishNumber is a special type of binary tree, with these properties:

• Firstly, it is a full binary tree. This means that if a node has children, it always has two children. We know this, because we’re told a FishNumber is always a pair.
• Secondly, we know that a FishNumber can either be a regular number, or contain another pair. Thus, each nodes in our tree can only be one of:
  • The parent of another pair.
  • An ordinary number.
  • A node cannot be both. Thus, all leaf nodes are ordinary numbers.

Let’s take a look at a bit of this solution’s FishNumber class:

class FishNumber:
    """ A FishNumber is either a leaf node or a pair of FishNumbers """
    
    EXPLODE_BRACKETS = 4
    SPLIT_MIN = 10
    
    def __init__(self, val=None):
        """ Create a new FishNumber. 
        If val is an int, then this is a leaf, and left/right will be None. """
        self.val: Optional[int] = val  # leaf node value
        self.left: Optional[FishNumber] = None
        self.right: Optional[FishNumber] = None
        self.parent: Optional[FishNumber] = None
    
    def __str__(self):
        if isinstance(self.val, int):
            return str(self.val)
        
        assert isinstance(self.left, FishNumber) and isinstance(self.right, FishNumber)
        return f"[{str(self.left)},{str(self.right)}]" # print recursively
    
    def __repr__(self):
        msg = str(self.val) if isinstance(self.val, int) else f"[{str(self.left)},{str(self.right)}]"           
        return msg if self.parent else "FishNumber(" + msg + ")"

    def fish_reduce(self):
        """ Reduce a FishNumber 
        - Explode any pairs that are more than four deep. Repeat explode until no more explosions possible.
        - Split any numbers that are > 10. Repeat split until no more splits are possible. """
        
        still_reducing = True
        while still_reducing:
            still_reducing = False  # assume nothing more to do
            
            # DFS through the tree, starting at the root, to see if we have pairs to explode
            stack = deque()
            stack.append((self, 0))    # (tree, depth)
            while len(stack) > 0:
                node, depth = stack.pop()

                # If we're at sufficient depth and this we're dealing with a pair
                if depth >= FishNumber.EXPLODE_BRACKETS and node.val is None:
                    self._explode(node)
                    still_reducing = True
                    break   # we've just exploded, so start loop again

                # otherwise, add children to the DFS frontier, ensuring left is always popped first
                if node.right and node.left: 
                    stack.append((node.right, depth + 1))
                    stack.append((node.left, depth + 1))

            if still_reducing:   # We've just exploded
                continue  # So loop
            
            # No explosions, so now try splitting
            assert not still_reducing, "Done exploding"
            assert len(stack) == 0, "Stack should be empty"
            stack.append(self)    # Add root node. We don't care about depth now.
            while len(stack) > 0:
                node = stack.pop()
                if node.val is not None:    # we've found our leaf
                    assert node.left is None and node.right is None
                    if node.val >= FishNumber.SPLIT_MIN:
                        self._split(node)
                        still_reducing = True
                        break   # back to the top
                else:   # not a leaf node, so must have children
                    stack.append(node.right)
                    stack.append(node.left)

    @staticmethod
    def parse(parse_input: list|int) -> FishNumber:
        """ Parse a list and convert to a FishNumber. 
        Recurses any nested lists, including leaf values. """
        node = FishNumber()
        if isinstance(parse_input, int):   # If a leaf node with no children
            node.val = parse_input
            return node

        assert len(parse_input) == 2, "Must be a pair in a list"
        node.left = FishNumber.parse(parse_input[0])
        node.right = FishNumber.parse(parse_input[1])
        node.left.parent = node
        node.right.parent = node

        return node   

A FishNumber is a node, and has four properties:

• val which is either an int if this FishNumber is a leaf (i.e. has no children); otherwise it is None.
• left and right, which are themselves FishNumber nodes, if val is None (and thus this FishNumber contains a pair).
• parent, which is only None for the root node.

We use the recursive static method parse() to create a FishNumber from a top-level list; it recurses into each nested item. This method doesn’t actually need to be part of the FishNumber class; it is static, meaning it doesn’t actually use or modify any FishNumber instance attributes; rather, it creates FishNumber instances. I could have created it as a separate function, independent of the FishNumber class. However, the creation of FishNumber is conceptually related to the FishNumber class. And for that reason, I’ve elected to make it a static method of the class.

We then use a Depth-First Search (DFS) to parse our tree, starting at the root node, and traversing all the way down to the bottom of the tree, from left to right. Note that the DFS is basically the same as the BFS that we’ve used before, but with one key difference: instead of popping FIFO (as we for BFS), or based on priority (as we do for Dijkstra), we’re popping last-in, first out (LIFO). I.e. the last thing we discovered in the frontier is the first thing we now explore further.

This is how the code works:

• For as long as we need to keep reducing:
  • We add the root node to a last-in, first-out (LIFO) deque frontier. We do this by appending a tuple, where the second parameter is the current depth.
  • While there are any nodes left in the frontier:
    • Pop the last item. (It pops left before right, because we’ll add them right before left.)
    • If the depth is sufficient and this is a pair, then explode and start the loop again.
    • Otherwise, if there are children, add them to the frontier, with depth of depth+1. Add the left item last, so it gets popped first.
  • If we haven’t exploded at this point, then try splitting.
    • Add the root to the LIFO frontier. This time, we don’t care about the depth.
    • While there are nodes left in the frontier:
      • Pop the last item.
      • If it’s a leaf, check if needs splitting. If so, split.
      • Otherwise, if there are children, add them to the frontier.

Now let’s look at how splitting works. This is the easy reduce operation. The objective is to remove a given node value, and replace it with a new pair. Thus, the current node becomes the parent of a new pair of leaf nodes.

    def _split(self, node):
        """ Split a single value into a pair of two halves.
        (Rounding down on the left, and rounding up on the right.)
        The current node becomes the parent of new left/right nodes. """
        assert node.val >= 10, "We can only split numbers >= 10"
        
        node.left = FishNumber(node.val//2) # new left val
        node.right = FishNumber(node.val - (node.val//2)) # new right val
        node.left.parent = node   # left node parent is current node
        node.right.parent = node  # right node parent is current node
        node.val = None  # current node value is cleared

The method does this:

• Splits the current node val in half, as required, and assigns the two halves to left and right.
• Because splitting increases the depth, we set this node as the parent for each of the new left and right values.
• We set this node’s val to None, since we can’t have a val as well as left and right.

Exploding is much more difficult.

We start from a node that is sufficiently nested and contains a pair of regular numbers. The goal is:

• Add our left number to the nearest next left number in the tree, regardless of how far up the tree we go.
• Add our right number to the nearest next right number in the tree, regardless of how far up the tree we go.

Let’s use this diagram to help explain it:

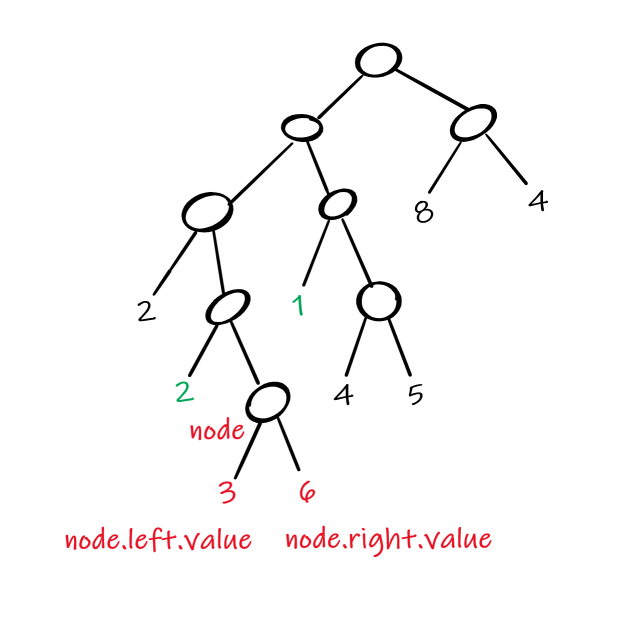
In this example:

• We’re starting with the node in red.
• We need to explode its left value ‘3’ into the nearest value to the left, which is ‘2’ (shown in green). The 2 gets replaced with 2+3=5.
• We need to explode its right value ‘6’ into the nearest value to the right, which is ‘1’ (shown in green). The 1 gets replaced with 1+6=7.
• Then we need to replace the node itself with 0.

The strategy is:

• We want to find a number on the left of our starting node:
  • From our starting node, keep moving UP the tree, until we reach a node that has a different left child to where we came from. Thus, if we were moving up from the left, we can’t go back down. But if we’re coming up from the right, we can.
  • If we get all the way to the top, and we’ve come up from the left, then there’s no left hand number for us to explode to.
  • If we get all the way to the top from the right, then there will always be a path on the left to go back down.
  • Now we go back DOWN the tree, until we reach a leaf value. If there’s a leaf on the right, we want that, since it’s closer to our left hand number.
• Now we want to find a number on the right. It’s basically the same process.
• Finally, we set the left and right for our starting node to None, and turn this node into a leaf with value of 0.

    def _explode(self, node: FishNumber):
        """ Split a pair. The node passed to this method itself contains a pair of leaf values.
        Left node value is added to first value on the left, if there is one.
        Right node value is added to first value on the right, if there is one.
        Current node value is then set to 0. 

        Args: node ([FishNumber]): The node containing a pair we need to explode
        """
        
        # First explode the left side
        prev_node = node.left
        current_node = node  # the parent of our pair of leaf values
        
        # Move UP the tree until we identify a node with a left (different) child
        # or until we can go no further
        while (current_node is not None and 
               (current_node.left == prev_node or current_node.left is None)):
            prev_node = current_node  # prev node moves up one
            current_node = current_node.parent  # current node now points to parent

        # Current node will be None if we previously reached the root from the left.
        # Otherwise, we must have identified a left node, so come back DOWN the left
        if current_node is not None:
            assert current_node.left is not None, "There must be a left node"
            current_node = current_node.left
            while current_node.val is None: # must have two children; keep going down until we reach a leaf
                if current_node.right is not None:
                    current_node = current_node.right   # if there's a number on the right of this node, it's nearest
                else:
                    current_node = current_node.left

            assert current_node.val is not None, "We've reached the value on the left"
            current_node.val += node.left.val   # add to the left

        # Now explode the right side
        prev_node = node.right
        current_node = node
        
        # traverse up the tree until we identify a node with a right (different) child
        # or until we can go no further
        while (current_node is not None and 
                (current_node.right == prev_node or current_node.right is None)):
            prev_node = current_node
            current_node = current_node.parent

        # current node will be null if we previously reached the root (so no right value)
        # otherwise, we must have identified a right node, so come back down the right
        if current_node is not None: 
            current_node = current_node.right
            while current_node.val is None:
                if current_node.left is not None:
                    current_node = current_node.left
                else:
                    current_node = current_node.right

            current_node.val += node.right.val  # add to the right

        # Final explode updates - set original node value to 0 and clear the children
        node.val = 0 
        node.left = None
        node.right = None

Finally, we need to be able to determine the magnitude. We can do this with recursion, just like before:

    def magnitude(self):
        """ Magnitude is given by 3*LHS + 2*RHS for any pair of values. 
        If the values are themselves lists, we must recurse.
        If the values are themselves ints, we return the int value. """
        if isinstance(self.val, int):
            return self.val

        assert self.left and self.right, "Must have children"
        return 3 * self.left.magnitude() + 2 * self.right.magnitude()

We run it like this:

with open(INPUT_FILE, mode="rt") as f:
    # Each input line is a nested list. 
    # Use literal_eval to convert each to a Python list.
    data = [literal_eval(line) for line in f.read().splitlines()]
    
# Part 1 - Sum all numbers and report magnitude
result = reduce(add, map(FishNumber.parse, data))  # Reduce to add n to n+1, then to n+2, etc
logger.info("Result = %s", result)
logger.info("Part 1 magnitude = %d", result.magnitude())

def add(left_tree: FishNumber, right_tree: FishNumber) -> FishNumber:
    """ Add two FishNumbers together.
    Creates a new parent node, with the supplied left and right set to its children. """
    new_root = FishNumber()
    
    new_root.left = left_tree
    new_root.right = right_tree
    new_root.left.parent = new_root
    new_root.right.parent = new_root
    
    new_root.fish_reduce()  # Note that this modifies the roiginal supplied FishNumbers
    return new_root

This is basically the same as Solution 1. I.e. we read in each FishNumber using literal_eval(). Then we use functools.reduce() to add each FishNumber to the next.

Part 2

This is basically the same as Part 2 for Solution #1.

mags = []
for perm in permutations(data, 2): # All permutations of 2 fish numbers
    # Quicker to parse the input data each time than deepcopy a FishNumber
    result = add(FishNumber.parse(perm[0]), FishNumber.parse(perm[1]))
    mags.append(result.magnitude())
    
logger.info("Part 2: max magnitude = %d", max(mags))

This solution runs about 8x quicker than Solution #1:

2022-01-25 21:56:40.267:INFO:__main__:  Result = [[[[7,7],[7,7]],[[7,8],[0,8]]],[[[8,9],[9,9]],[7,7]]]
2022-01-25 21:56:40.268:INFO:__main__:  Part 1 magnitude = 3869
2022-01-25 21:56:47.176:INFO:__main__:  Part 2: max magnitude = 4671
2022-01-25 21:56:47.179:INFO:__main__:  Execution time: 2.0004 seconds

‹›