Learning Python with Advent of Code Walkthroughs
Dazbo's Advent of Code solutions, written in Python

Advent of Code 2021 - Day 12
Useful Links
Concepts and Packages Demonstrated
Breadth First Search (BFS)pathlibgraphsnetworkxmatplotlib
Problem Intro
A little bit tricky, this one.
I’ve created two solutions for this:
- Solution #1 - Manually building a graph using an adjacency dictionary
- Solution #2 - Using NetworkX to facilitate building the graph, and to visualise
- Visualisation - The visualisation code
We’re told we’re navigating a cave system which contains large caves (denoted by uppercase labels) and small caves (denoted by lowercase labels).
The input data looks something like this:
start-A
start-b
A-c
A-b
b-d
A-end
b-end
And if we map out these connections, they can be visualised like this:
start
/ \
c--A-----b--d
\ /
end
Part 1
We’re asked to find the number of distinct paths that start at start and end at end, and don’t visit any small caves more than once.
Solution #1
This is the no frills solution.
Whenever we need to find all the paths from one point to another, a BFS should immediately come to mind as a possible way to solve the problem. The BFS is an algorithm we can always use to find all paths between two points. The tricky addition to this problem is that the small caves are one-way gates.
Setup
Nothing new here:
import logging
import os
import time
from collections import defaultdict, deque
logging.basicConfig(format="%(asctime)s.%(msecs)03d:%(levelname)s:%(name)s:\t%(message)s",
datefmt='%H:%M:%S')
logger = logging.getLogger(__name__)
logger.setLevel(level=logging.INFO)
SCRIPT_DIR = os.path.dirname(__file__)
INPUT_FILE = "input/input.txt"
# INPUT_FILE = "input/sample_input.txt"
The solution
Now we need to build a graph. In computing (and maths), a graph is a finite set of vertices (aka nodes or points), which are connected by edges (aka links).
If the edges have a direction, they are represented as arrows, and the graph is a directed graph. If the direction doesn’t matter, then edges are represented as lines, and the graph is an undirected graph. An undirected graph looks something like this:
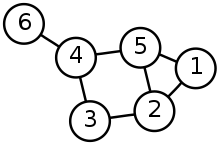
Here, it makes sense to represent our network of caves as an undirected graph, and then to find all the unique paths through it, given the “small caves” constraint.
We start by creating our CaveGraph class:
class CaveGraph():
""" Stores pairs of connected caves, i.e. edges.
Determines all caves from supplied edges.
Determines which caves are small, and which are large.
Creates a lookup to obtain all caves linked to a given cave.
Finally, knows how to determine all unique paths from start to end,
according to the rules given. """
START = "start"
END = "end"
def __init__(self, edges:set[tuple[str, str]]) -> None:
""" Takes a set of edges, where each edge is in the form (a, b) """
self.start = CaveGraph.START
self.end = CaveGraph.END
self._edges: set[tuple[str, str]] = set(edges)
self._nodes: set[str] = set()
self._small_caves: set[str] = set()
self._large_caves: set[str] = set()
self._determine_caves() # populate the empty fields
# Create lookup (adjacency) dict to find all linked nodes for a node
self._node_map: dict[str, set[str]] = defaultdict(set)
for x,y in edges: # E.g. x, y
self._node_map[x].add(y)
self._node_map[y].add(x)
assert self.start in self._node_map, "Start needs to be mapped"
assert self.end in self._node_map, "Finish needs to be mapped"
@property
def edges(self):
""" All the edges. An edge is one cave linked to another. """
return self._edges
@property
def small_caves(self):
""" Caves labelled lowercase. Subset of self.caves. """
return self._small_caves
@property
def large_caves(self):
""" Caves labelled uppercase. Subset of self.caves. """
return self._large_caves
def _determine_caves(self):
""" Build a set of all caves from the edges.
This will also initialise small_caves and large_caves """
for edge in self._edges:
for cave in edge:
self._nodes.add(cave)
if cave not in (self.start, self.end):
if cave.islower():
self._small_caves.add(cave)
else:
self._large_caves.add(cave)
def _get_adjacent_caves(self, node: str) -> set[str]:
""" Returns the adjacent caves, given a cave input. """
return self._node_map[node]
Things to say about this:
- First, the
__init__()method:- We can see it expects to be initialised using a
setof pairs of locations. I.e. a set of edges, where each edge is in the form of two nodes (which are caves). - It stores all the edges as
_edges. - It then runs
_determine_caves(), which:- Iterates through all the edges.
- For each edge, looks at each cave in the pair.
- Adds the edge (the cave) to
_caves. We’re using sets, which only store unique values. So if we add the same cave more than once, it doesn’t matter. - Checks if the cave is small or large, and adds to
_small_cavesand_large_caves, respectively. - Note how we’re once again prefixing all class variables and methods with
_, where they are only intended to be used by the object, and are not intended to be accessed outside the object.
- Now we create an
adjacency dictionary, which is basically a dictionary that maps each node (cave) to every other node (cave) that it is linked to. We do this using adefaultdict(set), i.e. a dict that it is initialised with an emptysetfor each key. That way, whenever we come across a cave that is linked to some cavex, we can simply add the new cave to the existing_node_map[x]set. - And that’s the graph built!
- We can see it expects to be initialised using a
- We add some properties for accessing the graph’s data. E.g.
edges,small_caves,large_caves. - We add a method that allows us to get all the adjacent caves for a given cave. This simply does a lookup using our adjacency dictionary.
Now let’s add the method that will do the hard work. I.e. actually performs the BFS:
def get_paths_through(self) -> set[tuple]:
""" Get all unique paths through from start to end, using a BFS """
start = (self.start, [self.start]) # (starting cave, [path with only start])
queue = deque()
queue.append(start)
unique_paths: set[tuple] = set() # To store each path that goes from start to end
while queue:
# If we popleft(), we do a BFS. If we simply pop(), we're doing a DFS.
# Since we need to discover all paths, it makes no difference to performance.
cave, path = queue.popleft() # current cave, paths visited
if cave == self.end: # we've reached the end of a desired path
unique_paths.add(tuple(path))
continue
for neighbour in self._get_adjacent_caves(cave):
new_path = path + [neighbour] # Need a new path object
if neighbour in path:
# big caves fall through and can be re-added to the path
if neighbour in (self.start, self.end):
continue # we can't revisit start and finish
if neighbour in self.small_caves:
continue # we can't revisit small cave
assert neighbour in self.large_caves
# If we're here, it's either big caves or neighbours not in the path
queue.append((neighbour, new_path))
logger.debug(new_path)
return unique_paths
This method is a fairly standard BFS, as we’ve used previously:
- We create a
starttuple, which has the first value set to ourstartcave, and the second value set to alistthat represents the path taken so far. Initially, thislistonly contains thestartcave. - We create a variable called
queue, which will be our frontier, implemented as adeque. - We add our
starttuple to the queue. -
We create a
setto store all unique paths found. - Now, as per the BFS pattern, whilst there are items remaining on the queue:
- Pop the next item.
- Evaluate if this next item is the
end. If it is:- Then we’ve found a new path, so we need to store it.
- Note that we convert the
listpath to atuplepath when we add it. We need to do this, becausesetsonly storehashableobjects;tuplesare hashable, butlistsare not. - Then
continue. (We don’tbreak, because we want to find all the paths.)
- Now find all adjacent caves, and for each:
- Add it to the current path.
- Determine if the adjacent cave is already in the path.
- If it is and it’s the start, end or small, then we can’t backtrack. So we don’t add it to the queue, and we move on to the next adjacent cave.
- If it adjacent cave was not already in the path, or was in the cave but was a big cave, then we can add it to the queue.
- When the queue is empty, we’ve now found all the paths.
We run it like this:
input_file = os.path.join(SCRIPT_DIR, INPUT_FILE)
with open(input_file, mode="rt") as f:
edges = set(tuple(line.split("-")) for line in f.read().splitlines())
graph = CaveGraph(edges) # Create graph from edges supplied in input
# Part 1
unique_paths = graph.get_paths_through()
logger.info("Part 1: unique paths count=%d", len(unique_paths))
Part 2
Now we’re told we’re allowed to visit any single small cave twice for any given path. Implementing this requires some thinking!!
My approach was to modify the get_paths_through() method to take a parameter small_cave_twice which defaults to False. If this is set to True, then the method allows the single revisit. Thus, we can use the same method for path parts. Of course, we need to modify the method itself:
def get_paths_through(self, small_cave_twice=False) -> set[tuple]:
""" Get all unique paths through from start to end, using a BFS
Args:
small_cave_twice (bool, optional): Whether we can
visit a small cave more than once. Defaults to False.
"""
start = (self.start, [self.start], False) # (starting cave, [path with only start], used twice)
queue = deque()
queue.append(start)
unique_paths: set[tuple] = set() # To store each path that goes from start to end
while queue:
# If we popleft(), we do a BFS. If we simply pop(), we're doing a DFS.
# Since we need to discover all paths, it makes no difference to performance.
cave, path, used_twice = queue.popleft() # current cave, paths visited, twice?
if cave == self.end: # we've reached the end of a desired path
unique_paths.add(tuple(path))
continue
for neighbour in self._get_adjacent_caves(cave):
new_path = path + [neighbour] # Need a new path object
if neighbour in path:
# big caves fall through and can be re-added to the path
if neighbour in (self.start, self.end):
continue # we can't revisit start and finish
if neighbour in self.small_caves:
if small_cave_twice and not used_twice:
# If we've visited this small cave once before
# Then add it again, but "use up" our used_twice
queue.append((neighbour, new_path, True))
continue
assert neighbour in self.large_caves
# If we're here, it's either big caves or neighbours not in the path
queue.append((neighbour, new_path, used_twice))
logger.debug(new_path)
return unique_paths
Here’s what’s changed:
- The frontier queue is no longer made up of
tuplesthat contain(cave, [path]). Now, thetuplehas a third value, which is whether we’ve used ourrevisitoption on this path yet. - Obviously, when we pop items off the queue, they will now unpack to three variables, not two, hence:
cave, path, used_twice. - Now, when we’re looking at neighbouring caves and we’ve found a cave already in the path, we need to do some additionally checking:
- Is it a small cave, and are we allowed to revisit a small cave, and have we already used our revisit? If yes, yes, no, then add this adjacent cave to the queue. But when we add it, flag that we’re using up our
revisitoption.
- Is it a small cave, and are we allowed to revisit a small cave, and have we already used our revisit? If yes, yes, no, then add this adjacent cave to the queue. But when we add it, flag that we’re using up our
And to run it:
# Part 2
unique_paths = graph.get_paths_through(small_cave_twice=True)
logger.info("Part 2: unique paths count=%d", len(unique_paths))
The output for both parts looks like this:
09:41:30.114:INFO:__main__: Part 1: unique paths count=5228
09:41:30.801:INFO:__main__: Part 2: unique paths count=131228
09:41:30.817:INFO:__main__: Execution time: 0.7296 seconds
Solution #2
This solution uses NetworkX. This is a pre-built library that allows us to create, manipulate, interrogate and render graphs. It can take a lot of the pain out of building graphs. It also has cool methods that allow us to do things like: find the shortest path from a to b.
Setup
First, we need to install NetworkX:
py -m pip install networks
And now our Python setup:
import logging
from pathlib import Path
import time
from collections import deque
import matplotlib.pyplot as plt
import networkx as nx
logging.basicConfig(format="%(asctime)s.%(msecs)03d:%(levelname)s:%(name)s:\t%(message)s",
datefmt='%H:%M:%S')
logger = logging.getLogger(__name__)
logger.setLevel(level=logging.INFO)
SCRIPT_DIR = Path(__file__).parent
INPUT_FILE = "input/input.txt"
# INPUT_FILE = "input/sample_input.txt"
RENDER = True
OUTPUT_DIR = Path(SCRIPT_DIR / "output/")
OUTPUT_FILE = Path(OUTPUT_DIR / "cave_graph.png") # where we'll save the animation to
Notes:
- I’ve decided to use
pathlib.Pathto handle operating system folder/file locations, rather than theosmodule. This was introduced in Python 3.4, and is considered a better way of manipulating paths, than theosapproach. Of note: you can use the/operator for joining paths, which is much more intuitive. - I’ve imported
networkx as nx. - I’ve imported
matplotlib.pyplot as plt. Matplotlib is a library for creating static, animated and interactive visualisations in Python, including graphs, charts and 3D models.
Solution
Our CaveGraph is a little shorter to implement:
class CaveGraph():
""" Stores pairs of connected caves, i.e. edges.
Determines all caves from supplied edges.
Determines which caves are small, and which are large.
Creates a lookup to obtain all caves linked to a given cave.
Finally, knows how to determine all unique paths from start to end,
according to the rules given. """
START = "start"
END = "end"
def __init__(self, edges:set[tuple[str, str]]) -> None:
""" Takes a set of edges, where each edge is in the form (a, b) """
self.start = CaveGraph.START
self.end = CaveGraph.END
self._graph = nx.Graph() # Internal implementation of the graph
self._graph.add_edges_from(edges) # Build the graph
self._small_caves: set[str] = set()
self._large_caves: set[str] = set()
self._categorise_caves() # populate the empty fields
assert self.start in self._graph, "Start needs to be mapped"
assert self.end in self._graph, "Finish needs to be mapped"
def _categorise_caves(self):
""" Build a set of all caves from the edges.
This will also initialise small_caves and large_caves """
for edge in self.edges:
for cave in edge:
if cave not in (self.start, self.end):
if cave.islower():
self._small_caves.add(cave)
else:
self._large_caves.add(cave)
@property
def edges(self) -> tuple[str,str]:
""" All the edges. An edge is one cave linked to another. """
return self._graph.edges
@property
def nodes(self):
return self._graph.nodes
@property
def small_caves(self):
""" Caves labelled lowercase. Subset of self.caves. """
return self._small_caves
@property
def large_caves(self):
""" Caves labelled uppercase. Subset of self.caves. """
return self._large_caves
def get_paths_through(self, small_cave_twice=False) -> set[tuple]:
""" Get all unique paths through from start to end, using a BFS.
Args:
small_cave_twice (bool, optional): Whether we can
visit a small cave more than once. Defaults to False.
"""
start = (self.start, [self.start], False) # (starting cave, [path with only start], used twice)
queue = deque()
queue.append(start)
unique_paths: set[tuple] = set() # To store each path that goes from start to end
while queue:
# If we popleft(), we do a BFS. If we simply pop(), we're doing a DFS.
# Since we need to discover all paths, it makes no difference to performance.
cave, path, used_twice = queue.popleft() # current cave, paths visited, twice?
if cave == self.end: # we've reached the end of a desired path
unique_paths.add(tuple(path))
continue
for neighbour in self._graph[cave]:
new_path = path + [neighbour] # Need a new path object
if neighbour in path:
# big caves fall through and can be re-added to the path
if neighbour in (self.start, self.end):
continue # we can't revisit start and finish
if neighbour in self.small_caves:
if small_cave_twice and not used_twice:
# If we've visited this small cave once before
# Then add it again, but "use up" our used_twice
queue.append((neighbour, new_path, True))
continue
assert neighbour in self.large_caves
# If we're here, it's either big caves or neighbours not in the path
queue.append((neighbour, new_path, used_twice))
logger.debug(new_path)
return unique_paths
Most of it is the same. But:
- We simply store the
_graphas annx.Graph()object. - We can initialise the graph using
nx.Graph.add_edges_from(edges), which takes all the edges, and establishes all the nodes, and all the adjacencies. So, we don’t need:- Our own adjacency dictionary.
- Our own
_determine_caves()method.
To solve for both parts, the code is nearly identical:
input_file = Path(SCRIPT_DIR, INPUT_FILE)
with open(input_file, mode="rt") as f:
edges = set(tuple(line.split("-")) for line in f.read().splitlines())
graph = CaveGraph(edges) # Create graph from edges supplied in input
logger.debug("Nodes=%s", graph.nodes)
logger.debug("Edges=%s", graph.edges)
# Part 1
unique_paths = graph.get_paths_through()
logger.info("Part 1: unique paths count=%d", len(unique_paths))
# Part 2
unique_paths = graph.get_paths_through(small_cave_twice=True)
logger.info("Part 2: unique paths count=%d", len(unique_paths))
Visualisation
Now let’s use NetworkX, in combination with Matplotlib, to render the output as an image.
Just add this to our CaveGraph class:
def render(self, file):
_ = plt.subplot(121)
pos = nx.spring_layout(self._graph)
# set colours for each node in the array, in the same order as the nodes
colours = []
for node in self.nodes:
if node in (CaveGraph.START, CaveGraph.END):
colours.append("green")
elif node in self.large_caves:
colours.append("blue")
else:
colours.append("red")
nx.draw(self._graph, pos=pos, node_color=colours, with_labels=True)
dir_path = Path(file).parent
if not Path.exists(dir_path):
Path.mkdir(dir_path)
plt.savefig(file)
This code:
- Defines a Pyplot plot area
- Uses NetworkX’s built in
spring_layout()method to create a set of node positions to be rendered, saved aspos. - We then create a
listofcolours, with the same number of items aspos. We use this to colour the nodes, based on their type, e.g. start/end, small cave, and big cave. - We then render the plot, using
nx.draw(), passing in the graph, the positions, the colours, and turning on labels. - Finally, we save the rendering as a file, creating the path if it doesn’t exist.
We call it like this:
if RENDER:
graph.render(OUTPUT_FILE)
I’m saving the file as a .ping. I’ve used the RENDER constant so that I can easily turn rendering on and off.
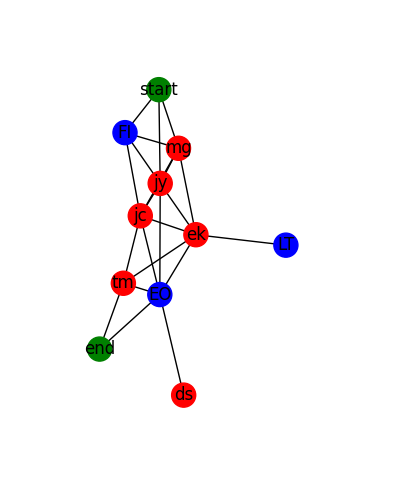
The rendered graph looks like this for the sample data:
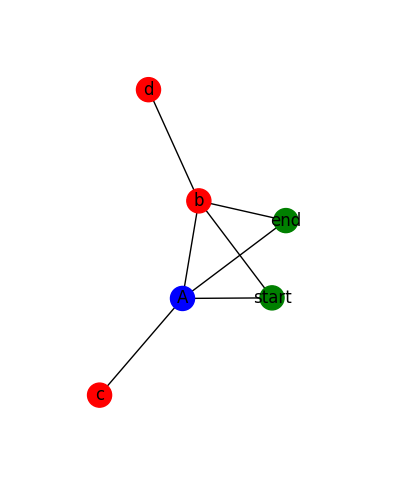
And it looks like this for actual data: