Learning Python with Advent of Code Walkthroughs
Dazbo's Advent of Code solutions, written in Python

Advent of Code 2021 - Day 8
Useful Links
Concepts and Packages Demonstrated
brute forcezipdefaultdictpermutations
Problem Intro
Not trivial, this one. My first approach worked fine, but it took me ages to work out the right process of elimination to process all the digits. The second solution is less complicated and less error-prone!
Here I’ve documented two different approaches to this problem:
- Solution #1 - Using sets and the structure of digits
- Solution #2 - Brute force mapping
We’re told that the sub’s four-digit display is malfunctioning. Each digit of the display is made up of 7 segments, labelled a through g. Each of the four digits has 7 output signal wires. Generating any given digit 0-9 is achieved by turning on the appropriate output signals, as shown here:
0: 1: 2: 3: 4: 5: 6: 7: 8: 9:
aaaa .... aaaa aaaa .... aaaa aaaa aaaa aaaa aaaa
b c . c . c . c b c b . b . . c b c b c
b c . c . c . c b c b . b . . c b c b c
.... .... dddd dddd dddd dddd dddd .... dddd dddd
e f . f e . . f . f . f e f . f e f . f
e f . f e . . f . f . f e f . f e f . f
gggg .... gggg gggg .... gggg gggg .... gggg gggg
Our problem is that the output wires have become scrambled. And worse than that, the scrambling is not consistent between digits on the four-digit display.
Our input data is given in the format of multiple lines, where each line contains:
- 10 unique signal patterns generated, i.e. signal outputs corresponding to digits 0-9 (but in no particular order)
- A 4 digit output we need to decode
So the input data looks like this:
be cfbegad cbdgef fgaecd cgeb fdcge agebfd fecdb fabcd edb | fdgacbe cefdb cefbgd gcbe
edbfga begcd cbg gc gcadebf fbgde acbgfd abcde gfcbed gfec | fcgedb cgb dgebacf gc
fgaebd cg bdaec gdafb agbcfd gdcbef bgcad gfac gcb cdgabef | cg cg fdcagb cbg
fbegcd cbd adcefb dageb afcb bc aefdc ecdab fgdeca fcdbega | efabcd cedba gadfec cb
...
Part 1
We’re asked to determine how many times any of the digits 1, 4, 7, or 8 appear in the output data. These are referred to as the easy digits, on the basis that these numbers are generated by unique numbers of output signals. E.g. if we look at the sample data and see an output signal be, then that must be generating a 1, because 1 is the only digit that is produced from just two signals.
Solution #1
This solution depends on us understanding the structure of each digit. E.g. we know that a 1 is composed of 2 segments, a 7 is composed of 3 segments, etc.
Our solution for part 1 is this:
- Read in the signals and output values into two lists of sorted strings. It’s good to sort them, because the signal patterns and output signals are in random signal order. If we sort them, it’s then easy to compare them.
- Store a dictionary that maps easy digits to signal counts.
- For each output digit, determine if they contain signal counts that correspond to an easy digit.
- Finally, count how many easy digits were produced.
unique_segment_counts = {2: 1, 4: 4, 3: 7, 7: 8} # {count: digit}
input_file = os.path.join(SCRIPT_DIR, INPUT_FILE)
with open(input_file, mode="rt") as f:
data = f.read().splitlines()
signals = [] # list of lists of sorted input values
outputs = [] # list of lists of sorted output values
for line in data:
digit_signals, four_digit_outputs = line.split("|")
signals.append(["".join(sorted(signal)) for signal in digit_signals.split()])
outputs.append(["".join(sorted(signal)) for signal in four_digit_outputs.split()])
# Part 1
all_easy_digits = []
for output_line in outputs:
# Determine which digits in the output are in 1, 4, 7, 8
easy_digits = [output for output in output_line if len(output) in unique_segment_counts]
all_easy_digits.append(easy_digits) # append, e.g. ['bcg', 'abcdefg', 'cg']
sum_of_easy_digits = sum([len(digits) for digits in all_easy_digits]) # count all
logger.info("Sum of easy digits: %d", sum_of_easy_digits)
Part 2
We’re asked to decode all the four-digit outputs, and add them all up. This requires us to be able to determine which digit is represented by each unique combination of segments, and then use this mapping to covert the digit outupts into digits.
The solution here relies on us knowing the structures of the digits. I.e.
- We already have 1, 4, 7, and 8 mapped.
- We can work out segment
a, since it’s in 7 but not 1.
0: 1: 2: 3: 4: 5: 6: 7: 8: 9:
aaaa .... aaaa aaaa .... aaaa aaaa aaaa aaaa aaaa
b c . c . c . c b c b . b . . c b c b c
b c . c . c . c b c b . b . . c b c b c
.... .... dddd dddd dddd dddd dddd .... dddd dddd
e f . f e . . f . f . f e f . f e f . f
e f . f e . . f . f . f e f . f e f . f
gggg .... gggg gggg .... gggg gggg .... gggg gggg
- We can propose candidates for segments
candf, since they’re the only segments in 1. We just don’t which one iscand which one isf. - Similarly, we can propose candidates for segments
bandd, since they’re in 4, but not in 7.
0: 1: 2: 3: 4: 5: 6: 7: 8: 9:
aaaa .... aaaa aaaa .... aaaa aaaa aaaa aaaa aaaa
b c . c . c . c b c b . b . . c b c b c
b c . c . c . c b c b . b . . c b c b c
.... .... dddd dddd dddd dddd dddd .... dddd dddd
e f . f e . . f . f . f e f . f e f . f
e f . f e . . f . f . f e f . f e f . f
gggg .... gggg gggg .... gggg gggg .... gggg gggg
- Now we have enough data to know the full set of segments that make up 3, since this is the only 5-segment digit that contains 1. (The other 5-segment digits are 2 and 5.)
0: 1: 2: 3: 4: 5: 6: 7: 8: 9:
aaaa .... aaaa aaaa .... aaaa aaaa aaaa aaaa aaaa
b c . c . c . c b c b . b . . c b c b c
b c . c . c . c b c b . b . . c b c b c
.... .... dddd dddd dddd dddd dddd .... dddd dddd
e f . f e . . f . f . f e f . f e f . f
e f . f e . . f . f . f e f . f e f . f
gggg .... gggg gggg .... gggg gggg .... gggg gggg
- We can determine which segment signal corresponsds to
d, since it’s the intersection of 3 and candidate segmentsb+d. Having identifiedd, we now know which segment signal wasb.
0: 1: 2: 3: 4: 5: 6: 7: 8: 9:
aaaa .... aaaa aaaa .... aaaa aaaa aaaa aaaa aaaa
b c . c . c . c b c b . b . . c b c b c
b c . c . c . c b c b . b . . c b c b c
.... .... dddd dddd dddd dddd dddd .... dddd dddd
e f . f e . . f . f . f e f . f e f . f
e f . f e . . f . f . f e f . f e f . f
gggg .... gggg gggg .... gggg gggg .... gggg gggg
- Digit 5 is the intersection of 5-segment digits 2+5 and segment
b. And now we know the segments for digit 2, as the only remaining 5-segment digit.
0: 1: 2: 3: 4: 5: 6: 7: 8: 9:
aaaa .... aaaa aaaa .... aaaa aaaa aaaa aaaa aaaa
b c . c . c . c b c b . b . . c b c b c
b c . c . c . c b c b . b . . c b c b c
.... .... dddd dddd dddd dddd dddd .... dddd dddd
e f . f e . . f . f . f e f . f e f . f
e f . f e . . f . f . f e f . f e f . f
gggg .... gggg gggg .... gggg gggg .... gggg gggg
- All that remains unmapped are the digits with 6 segments, i.e. 0, 6 and 9.
- Of these, only digit 9 includes digit 4, so we can identify the set for 9. That leaves only 0 and 6 unmapped.
- We can determine the segment set for digit 0, since it’s the only one of 0 and 6 that contains d.
- And finally, that just leaves digit 6.
Implementing all of this in Python is easily achieved using sets, since we can use set algebra to determine when one set contains another set, any intersection of sets, any difference between sets, and any union that is created by combining sets.
| Set Relationship | Looks like |
|---|---|
| Union (&) | 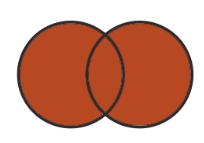 |
| Intersection(&) | 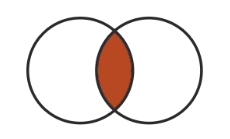 |
| Difference (-) | 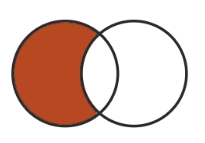 |
| Superset/Contains (>) |
So finally, here’s the code:
# Part 2
outs = []
for i, input_line in enumerate(signals):
signal_map = determine_signal_map(input_line)
outs.append(int("".join([str(signal_map[output]) for output in outputs[i]])))
logger.info("Sum of outputs: %d", sum(outs))
def determine_signal_map(input_line):
""" Return a dict that maps the str representation of the segments to the digit they produce """
segments = {} # {segment: set(inputs)}
seg_candidates = {} # {segment: set(inputs)}
# create a list, containing a set of signals for each (unknown) unique digit
digit_signals = [set(input) for input in input_line]
# First let's map the easy digits to segment sets, in the form {digit: set(signals)}
# We know 1, 4, 7, 8. E.g. {1: {'g', 'c'}, ...}
known_digits = {unique_segment_counts[len(input)]: set(input)
for input in input_line if len(input) in unique_segment_counts}
segments["a"] = known_digits[7] - known_digits[1] # a is in 7, but not in 1
seg_candidates["b"] = seg_candidates["d"] = known_digits[4] - known_digits[7] # b, d are in 4 but not in 7
seg_candidates["c"] = seg_candidates["f"] = known_digits[1] # c, f are in 1
unknown_digits_with_five_segments = [digit for digit in digit_signals if len(digit)==5] # 2, 3, 5
known_digits[3] = [digit for digit in unknown_digits_with_five_segments
if digit > known_digits[1]][0] # Only digit 3 contains digit 1
unknown_digits_with_five_segments.remove(known_digits[3]) # Leaving 2, 5
segments["d"] = seg_candidates.pop("d") & known_digits[3]
segments["b"] = seg_candidates.pop("b") - segments["d"]
# 5 contains b (known); whilst 2 doesn't. 5 contains f (unknown)
known_digits[5] = [digit for digit in unknown_digits_with_five_segments
if digit > segments["b"]][0]
unknown_digits_with_five_segments.remove(known_digits[5]) # Leaving 2.
known_digits[2] = unknown_digits_with_five_segments[0]
unknown_digits_with_six_segments = [digit for digit in digit_signals if len(digit)==6] # 0, 6, 9
known_digits[9] = [digit for digit in unknown_digits_with_six_segments
if digit > known_digits[4]][0] # 9 is the only one that contains 4
unknown_digits_with_six_segments.remove(known_digits[9]) # 0, 6 remaining
known_digits[6] = [digit for digit in unknown_digits_with_six_segments
if digit > segments['d']][0] # 6 is the only one that contains segment d
unknown_digits_with_six_segments.remove(known_digits[6]) # 0 remaining
known_digits[0] = unknown_digits_with_six_segments[0]
# convert back to strings and transpose to {str: digit}
return {"".join(sorted(input)): digit for digit, input in known_digits.items()}
It’s pretty quick. The output looks like this:
2022-01-13 08:29:59.815:INFO:__main__: Sum of easy digits: 421
2022-01-13 08:29:59.818:INFO:__main__: Sum of outputs: 986163
2022-01-13 08:29:59.818:INFO:__main__: Execution time: 0.0048 seconds
Solution #2
This solution is a tiny bit slower, but it doesn’t require any prior knowledge of the structure of any digits. We’re going to use a brute force solution, where we try every possible combination of segment signals, and find the combination that works for each line of input.
Setup
import logging
import os
import time
from collections import defaultdict
from itertools import permutations
Here we’re going to use:
Solution
We start by creating a constant called SEGMENTS, which contains all the valid segments. Then we create VALID_DIGITS, which is a dictionary that maps each correct combination of segment signals to the outputs they should produce.
Then we read in the data as before.
SEGMENTS = "abcdefg"
# These are the output signal segment combinations that are valid
VALID_DIGITS = {
"abcefg": 0,
"cf": 1,
"acdeg": 2,
"acdfg": 3,
"bcdf": 4,
"abdfg": 5,
"abdefg": 6,
"acf": 7,
"abcdefg": 8,
"abcdfg": 9
}
input_file = os.path.join(SCRIPT_DIR, INPUT_FILE)
with open(input_file, mode="rt") as f:
data = f.read().splitlines()
signals = [] # list of lists of sorted segment signals for all digits
outputs = [] # list of lists of 4 * sorted output values
for line in data:
digit_signals, four_digit_outputs = line.split("|")
signals.append(["".join(sorted(signal)) for signal in digit_signals.split()])
outputs.append(["".join(sorted(signal)) for signal in four_digit_outputs.split()])
We create a defaultdict called simple_digit_counts, where each member will be a list. The great thing about using the defaultdict is that we don’t need to initialise any new lists for any new keys in the dict. If we try to append to a list referenced by a key we haven’t used before, then the defaultlist will create an empty list for us. So we don’t get any key errors!
We then go through all the valid digit strings, using the length of each as the key for the digit_counts dict. The value ends up being a list containing all the digit segment strings that are of that length.
We then use list comprehension to build a new list using the values from the dictionary we just created, where the length of the value is 1. I.e. all the digits made up of a unique number of segments. This is just a clever way to get the segment strings for the easy digits 1, 4, 7, and 8.
# Count how many segments are used for each digit
digit_counts = defaultdict(list)
for digit_segments in VALID_DIGITS:
# store as {count: [digit_segments]}, e.g. 2: ['cf'], 5: ['acdeg', 'acdfg', 'abdfg']
digit_counts[len(digit_segments)].append(digit_segments)
# filter simple_digits to include only ["cf", "bcdf", "acf", "abcdefg"]:
simple_digits = [v[0] for k, v in digit_counts.items() if len(v) == 1]
Now the good stuff happens:
We iterate through each row of input data. For each row, we iterate through the 5040 permutations (7!) of segment combinations that can be made from 7 segment signals. This is done using itertools.permutations() to obtain all the unique ways of ordering any set of items.
For example, consider all the ways we might order the three characters “abc”:
perms = permutations("abc")
print("\n".join(str("".join(perm)) for perm in perms))
As the output shows, there are 3! = 3x2x1 = 6 ways of ordering these letters:
abc
acb
bac
bca
cab
cba
For the current permutation of 7 signals, we map each each segment in the permutation to “abcdefg”, using zip(). Recall that zip() takes any number of identical-length iterables, and produces produces a list of list of tuples, where each tuple contains one element from each of the input iterables. In this case, we turn those tuples into a dictionary.
For example, if the current permutation is “cfbadge”, then we could print the current unscramble_map as follows:
for k, v in unscramble_map.items():
print(f"{k}: {v}")
This prints:
a: c
b: f
c: b
d: a
e: d
f: g
g: e
So now we have a way to convert from scrambled segment signals to unscrambled segment signals. But only one permutation of segment signals will yield valid digits when we decode the input segments of any given input line. So we take each of the 10 input signal words of the current input line, and decode them using our map. If the decoding of any input word doesn’t yield one of our VALID_DIGITS then we know this permutation is no good, and we can move on to the next permutation.
We’re also using a try-except block to continue to the next permutation. We can’t simply use continue, since this would only continue to the next word in the input data.
If we’ve tried every word in the input signals and they’ve all been unscrambled to valid digit, then we’ve found the unique permutation of segment signals that is required for this line of data. So we can use our unscramble map to decode each of the four output digits.
We check if each unscrambled output digit is in the easy digits, to solve Part 1.
Finally, to solve Part 2:
- Take each of our unscrambled output digits, and look up the digit value using
VALID_DIGITS. - Join the four digits together, and then convert to an
intvalue. - Sum all the
intvalues, as we’ve been asked to do.
count_simple_digits_in_output = 0
numeric_outputs = []
# process each row of data; different rows require different perms
for row_num, input_row in enumerate(signals):
# Only one permutation will be valid for any given line
for perm in permutations(SEGMENTS): # e.g. "cfbadge"
unscramble_map = dict(zip(SEGMENTS, perm))
try: # use try-except pattern for continuing outer loop
for word in input_row:
unscrambled_word = unscramble(word, unscramble_map)
if unscrambled_word not in VALID_DIGITS:
raise StopIteration # if any unscrambled not in valid
except StopIteration:
continue # continue to next permutation
# If we're here, then we've got a permutation that maps to valid digits
numeric_output = []
for word in outputs[row_num]:
unscrambled_word = unscramble(word, unscramble_map)
# check if in ("cf", "bcdf", "acf", "abcdefg"):
if unscrambled_word in simple_digits:
count_simple_digits_in_output += 1
# convert from segments to digit, and append the digit
numeric_output.append(VALID_DIGITS[unscrambled_word])
numeric_outputs.append(int("".join(map(str, numeric_output)))) # convert to 4-digit int
break # If we've got here, we've got everything we need. No more perms needed.
logger.info("Part 1 - Sum of easy digits: %d", count_simple_digits_in_output)
logger.info("Part 2 - Sum of numeric outputs=%d", sum(numeric_outputs))
For completeness, here’s our unscramble() function:
def unscramble(word, unscramble_map: dict) -> str:
""" Takes a scrambled input word, and converts to unscrambled.
Args:
word (str): Scrambled input
unscramble_map (dict): Map of scrambled char->unscrambled char """
return "".join(sorted([unscramble_map[char] for char in word]))
And finally, let’s test our new solution:
2022-01-13 20:02:18.075:INFO:__main__: Part 1 - Sum of easy digits: 421
2022-01-13 20:02:18.076:INFO:__main__: Part 2 - Sum of numeric outputs=986163
2022-01-13 20:02:18.076:INFO:__main__: Execution time: 0.7756 seconds
So, it’s about 150x slower than Solution #1. But still pretty quick, and I like it a lot more!