Learning Python with Advent of Code Walkthroughs

Dazbo's Advent of Code solutions, written in Python

No Time for a Taxicab

Advent of Code 2016 - Day 1

Day 1: No Time for a Taxicab

Useful Links

›

Concepts and Packages Demonstrated

Unit CircleTaxicab Geometrylist.count()Loggingos.pathtime.perf_counter

Problem Intro

Welcome to Advent of Code 2016, Day 1! In this puzzle, you’re airdropped near Easter Bunny Headquarters in a city with a grid-like street layout. You start at coordinates (0,0) facing North. You’re given a sequence of instructions, each telling you to either turn left (L) or right (R) 90 degrees, and then walk forward a specified number of blocks.

The input data looks like a comma-separated string of instructions, for example:

R2, L3, R2, R2, R2, R5, L5, R5, R3

Part 1

How many blocks away is Easter Bunny HQ?

For Part 1, the goal is to determine the “taxicab distance” (also known as Manhattan distance) to the final destination after following all instructions. This means summing the absolute differences of the final X and Y coordinates from the starting point (0,0).

My solution uses a location dictionary to keep track of the current x and y coordinates, and a heading variable (0 for North, 90 for East, 180 for South, 270 for West) to represent the current direction.

The core logic resides in the process_direction function:

def process_direction(location: dict, visited_locations: list, heading: int, instr: str):
    turn = instr[0]
    magnitude = int(instr[1:])
    rotation = 90 if turn == 'R' else -90
    heading = convert_angle(heading + rotation)
    
    # We need to process the instruction one unit at a time, 
    # so that we store the path taken, not just the final landing location of each instruction
    for _ in range(magnitude):
        # unit circle geometry
        location[X] += round(sin(radians(heading)))
        location[Y] += round(cos(radians(heading)))
        
        # store all coords visited whilst following this direction
        visited_locations.append(location.copy())
    
    return location, heading

def convert_angle(angle: int):
    """ Convert any angle to %360

    Args:
        angle (int): An angle

    Returns:
        [int]: The angle
    """
    if (angle < 0):
        angle += 360
    
    return angle % 360

Unit Circle

To determine the change in our x and y coordinates, we can use the concept of a unit circle. A unit circle is a circle with a radius of 1, centered at the origin (0,0) of a Cartesian plane.

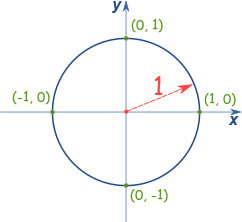
Unit Circle

In our solution, we represent the direction of travel as a heading in degrees: 0° for North, 90° for East, 180° for South, and 270° for West. We can use trigonometry to determine the change in x and y for each step we take.

Let’s look at how this works for our four cardinal directions:

This is exactly what we need to update our coordinates as we move one block at a time. The Python code uses the math.sin and math.cos functions, which work with radians, so we convert our degree heading to radians before using them.

After all instructions are processed, the taxicab distance is simply abs(final_x) + abs(final_y).

Part 2

What is the distance to the first location you visit twice?

For Part 2, the challenge is to find the very first location that is visited more than once. This includes all intermediate steps taken during movement.

My solution addresses this by maintaining a visited_locations list. As shown in the process_direction function above, for each block walked, the current location is appended to this list. This creates a complete history of the path taken.

A Note on copy()

You might have noticed the use of location.copy() when appending to the visited_locations list. This is a crucial detail. In Python, dictionaries are mutable objects. If we had simply appended location directly, we would be appending a reference to the location dictionary. This means that every time the location dictionary was updated, all the entries in visited_locations would also change, because they would all be pointing to the same single dictionary object. By the end, visited_locations would just contain the final location repeated many times.

By using .copy(), we create a shallow copy of the dictionary at that moment in time. This new dictionary object is then appended to the list, preserving the coordinates at that specific step. This ensures that visited_locations contains a true history of the path taken, with each entry being a distinct snapshot of the coordinates at each point along the way.

After processing all instructions, the code iterates through the visited_locations list to find the first coordinate that appears more than once. The list.count() method is used for this purpose.

    for visited in visited_locations:
        # we want the first location that was visited twice
        # i.e. where this particular location has a count > 1
        if visited_locations.count(visited) > 1:
            taxicab_distance = abs(visited[X]) + abs(visited[Y])
            logging.info(f"First location visited twice was {visited}")
            logging.info(f"Distance to this location: {taxicab_distance}")
            break

The list.count(element) method returns the number of times element appears in the list. By iterating through visited_locations and checking count(visited) > 1, the first such visited location found is the answer to Part 2.

Results

The execution of the solution yields results that look something like this:

Taxicab distance for entire journey: 230
First location visited twice was {'x': 116, 'y': 5}
Distance to this location: 121
Execution time: 0.0059 seconds

›