Advent of Code 2015 - Day 24

Day 24: It Hangs in the Balance

Useful Links

‹›

• 2015 Main Page
• My solution code

Concepts and Packages Demonstrated

ComprehensionsCombinationsassert

Page Navigation

• Problem Intro
• Part 1
• Part 2
• Results

Problem Intro

This one was fun! And not too tricky.

We’re told we need to load up the sleigh, by splitting all packages into three groups of equal weight. The three groups will be placed into three locations on the sleigh:

1. The passenger compartment.
2. A container to the left of the passenger compartment.
3. A container to the right of the passenger compartment.

To allow room for Santa’s legs, the group of packages going in the passenger compartment needs to have as few packages as possible. Furthermore, if there are multiple ways to arrange the groups such that the passenger compartment has the fewest packages, then we need to select the configuration with the lowest quantum entanglement of the passenger group. Quantum entanglement is defined as the products of weights in that group.

Our input is the sorted list of all package weights, e.g.

1
2
3
4
5
7
8
9
10
11

Part 1

What is the quantum entanglement of the first group of packages in the ideal configuration?

Here’s my strategy:

• First, add up all the package weights, and divide by 3. This gives us the required weight for each group.
• We actually only care about the packages that we put into the passenger group. The configurations of the two other packages are irrelevant.
• Can we get to the target weight with any 1 package? Now try with any 2 packages? How try with any 3 packages? And so on. As soon as we find a valid combination of packages that meets our target weight, break from our loop.
• It’s possible that we might have returned more than one valid combination of packages. If so, return the combination with the lowest QE.

Actually, my solution is very similar to the solution I did for Day 16. The heart of the solution is to use combinations to obtain all combinations of packages that sum to the required weight. We do this in a loop, trying combinations with one package, then two, then three, and so on.

Here’s where most of the work happens:

def distribute_packages(package_weights, number_of_groups) -> tuple:
    logger.info(f"Solving for {number_of_groups} groups")
    
    package_count = len(package_weights)
    total_weight = sum(package_weights)
    target_weight_per_group = total_weight // number_of_groups
    
    logger.info(f"Total packages: {package_count}, with total weight: {total_weight}")
    logger.info(f"Target weight per bag: {target_weight_per_group}")

    # Get all combos for first group.
    # Try any single package, then any two packages, then any three, etc
    # Since we need fewest packages that add up to target weight,
    # there's no point trying more than package_count // number_of_groups
    valid_combos = None
    for num_packages in range(1, (package_count // number_of_groups) +1):
        logger.debug("Trying %d packages...", num_packages)
        valid_combos = [combo for combo in list(combinations(package_weights, num_packages))
                              if sum(combo) == target_weight_per_group]
        if valid_combos: # we've found a solution
            break
    
    assert valid_combos, "There should be a matching combo"
    logger.debug(valid_combos)

    return min(valid_combos, key=get_quantum_entanglement)

def get_quantum_entanglement(bag: tuple):
    """ QE = the product of the values in the tuple """
    return prod(bag)

Some other points to mention:

• I break from the loop, as soon as we find a valid combination.
• I assert that, having exited the loop, we have found at least one valid combination of packages.
• It’s possible that we have more than one valid combination of packages. In which case, we need to pick the one with the lowest QE. To do this, I use min(), and pass in our get_quantum_entanglement() function as the key. The great thing about aggregation functions like min() is that we can pass any function to them, to be used as the function that should be applied to every member of a collection passed to it.

We can then solve for Part 1:

def main():
    with open(locations.input_file, mode="rt") as f:
        package_weights = [int(x) for x in f.read().splitlines()]
    
    logger.debug(f"Package weights: {package_weights}")

    run_part(1, package_weights, 3)
    
def run_part(part: int, package_weights, number_of_groups: int):
    optimum_solution = distribute_packages(package_weights, number_of_groups)
    logger.info("Part %d:", part)
    logger.info(f"First group: {optimum_solution}")
    logger.info(f"QE: {get_quantum_entanglement(optimum_solution)}")
    logger.info(".")

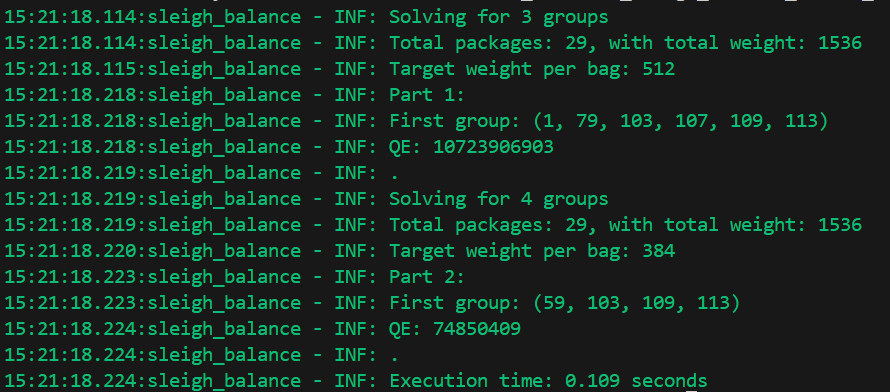
With our sample input data, the results look like this:

Part 2

Same as before, but now we have four groups, not three. As before what is the quantum entanglement of the first group of packages in the ideal configuration?

So trivial! I can just pass in 4 groups, rather than 3:

    run_part(2, package_weights, 4)

Results

I’m pleased with this. The code is simple, short, and pretty quick. It runs in about 0.1 seconds with the real input data.

‹›