Advent of Code 2015 - Day 20

Day 20: Infinite Elves and Infinite Houses

Useful Links

Concepts and Packages Demonstrated

Problem Intro
Part 1
Part 2
Results

Problem Intro

An infinite number of elves have been tasked with delivering presents to an infinite number of houses, numbered sequentially as 1, 2, 3, etc. Each elf is numbered, and elves deliver to houses that are a multiple of their elf identifier. E.g.

Elf #1 delivers to houses 1, 2, 3, 4, etc.
Elf #2 delivers to houses 2, 4, 6, 8, etc.
Elf #3 delivers to houses 3, 6, 9, 12, etc.

When an elf visits a given house, it delivers ten times as many presents as its elf identifier. Thus:

House   Elf 1   Elf 2   Elf 3   Elf 4   Elf 5   Elf 6   Running Total
1       10      -       -       -       -       -       10
2       10      20      -       -       -       -       30
3       10      -       30      -       -       -       40
4       10      20      -       40      -       -       70
5       10      -       -       -       50      -       60
6       10      20      30      -       -       60      120

Part 1

What is the lowest house number of the house to get at least as many presents as the number in your puzzle input?

From the table above, we can see that each house is visited by all the elf numbers that are factors of that house number. In case you need a reminder: the factors of any given number are the integer values that the number is divible by, leaving no remainder. For example, we can identify the factors of the number 8 as follows:

Integer	8 integer divided by integer	Remainder	Is a factor?
1	8	0	Yes
2	4	0	Yes
3	2	2	No
4	2	0	Yes
5	1	3	No

There’s no point in counting any higher, since no number greater than 4 (i.e. 8\\2) can be a factor of 8.

In fact, it turns out that we never need to test integer values greater than the square root of 8. Why? Because if we divide our number by any factor that is smaller than the square root of our number, then the result will be the complementary factor that is larger than the square root. For example, the square root of 8 is approximately 2.83. The largest possible integer we need to test is 2. We can divide 8 by 2, and the result is 4. Thus, 4 is a factor of 8. Similarly, 8 is a factor of 8, but we already determined that when we divided 8 by 1.

Why am I telling you all this? Because it turns out that for any given house number h, the number of presents delivered to that house will be the result of the sum of 10f, for each factor f of h.

First, let’s create a function that returns all the factors, for a given house number:

def get_factors(num: int) -> set[int]:
    """ Gets the factors for a given number. Returns a set[int] of factors. 
        # E.g. when num=8, factors will be 1, 2, 4, 8 """
    factors = set()

    # Iterate from 1 to sqrt of 8,  
    # since a larger factor of num must be a multiple of a smaller factor already checked
    for i in range(1, int(num**0.5) + 1):  # e.g. with num=8, this is range(1, 3)
        if num % i == 0: # if it is a factor, then dividing num by it will yield no remainder
            factors.add(i)  # e.g. 1, 2
            factors.add(num//i)  # i.e. 8//1 = 8, 8//2 = 4
    
    return factors

It works as follows:

Create a set to store our factors.
Obtain a range that returns all integers that are smaller than the square root of the supplied number. (Note that raising any number to the power of 1/2 is the same as taking the square root of that number.)
For each integer value returned by this range, test if it is factor by dividing num by this integer. If num is exactly divisible by the this integer, then the integer is a factor. Furthermore, the quotient of the division is also a factor. So we add both factors to our set.

Actually, this seems like a useful reusable function, so I’ve moved it into by type_defs.py module.

Now we call it, like this:

    # Part 1
    presents_dropped, house_num = 0, 0
    while presents_dropped < TARGET:
        house_num += 1
        presents_dropped = sum(factor * 10 for factor in td.get_factors(house_num))  
        logger.debug("House=%d, presents dropped=%d", house_num, presents_dropped)    

    logger.info("Part 1: House=%d, presents dropped=%d", house_num, presents_dropped)

This works as follows:

We loop until the number of presents dropped exceeds our target.
Increment house_num, and then pass this house_num to td.get_factors(), which returns all the factors for this house number.
Multiply each factor by 10, to give us the number of presents dropped by a given elf.
Sum up these values, to give the total number of presents dropped at this house.

If we set our target as 200, the result looks like this:

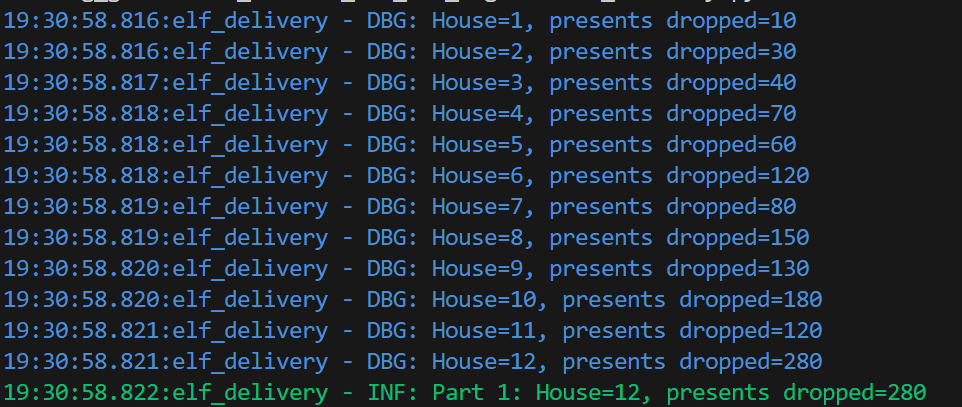
Elf drops, Part 1

Great! So far, so good.

Part 2

The elves now each visit a maximum of 50 houses, and each elf drops a number of presents equal to 11 times their elf number, at each house.

As before:

What is the lowest house number of the house to get at least as many presents as the number in your puzzle input?

My amended strategy is:

Count the occurences of each factor, because each factor represents an elf visit to any house.
When an elf reaches its limit of visits, then ignore this elf factor when calculating present drops.

Here’s the code:

def generate_presents_for_house(per_elf_multiplier: int, elf_visit_limit: int = 0):
    """ Generator function that returns the number of presents dropped at a given house.

    Yields:
        [tuple]: Current house number, total presents dropped at this house
    """
    house_num = 0
    elf_visits = defaultdict(int)

    while True: # iterate for each house, yielding each time
        house_num += 1
        presents_dropped = 0
        factors_for_house = td.get_factors(house_num)
        
        # iterate through all the factors for this house
        for factor in factors_for_house:
            if elf_visit_limit and elf_visits[factor] >= elf_visit_limit:
                pass
            else:
                elf_visits[factor] += 1
                presents_dropped += factor * per_elf_multiplier
      
        if logger.isEnabledFor(logging.DEBUG): # avoid expensive sorting
            logger.debug("House %d visited by: %s", house_num, sorted(factors_for_house))
            logger.debug("Presents dropped: %d", presents_dropped)
        
            # convert defaultdict to dict so we don't print out the default factory information
            logger.debug("Factors counter: %s", dict(elf_visits)) 
        
        yield house_num, presents_dropped

A few points to note:

My function is a generator.
- It has a yield statement rather than return statement.
- It works like an iterator, but - as a generator - it returns each successive value on-the-fly, i.e. returning a single value with each call. It doesn’t need to pre-calculate all values.
- It persists state between successive calls. So, we can keep track of our elf visits, even between successive calls to the generator.
I’m using a defaultdict to count the number of visits for a given elf. That way, we can increment every time we see a given elf number, but we don’t have to initialise the dictionary.
I’m using the same td.get_factors(house_num) as Part 1.
The debug logging statements are expensive, because they are called frequently, and involve a sort. Even if I set the debug level to INFO, the variables within the logger.debug() statements are still evaluated; even though they are not printed! So, I’ve added a logging level check around these debug statements. It makes a big difference to the overall performance!!

We call the generator function like this:

    # Part 2
    gen = generate_presents_for_house(11, MAX_HOUSES_PER_ELF)
    presents_dropped, house_num = 0, 0
    while presents_dropped < TARGET:
        house_num, presents_dropped = next(gen)
    
    logger.info("Part 2: House=%d, presents dropped=%d", house_num, presents_dropped)

To test, I’m going to use these values:

logger.setLevel(logging.DEBUG)
TARGET = 200
MAX_HOUSES_PER_ELF = 5

And the output looks like this:

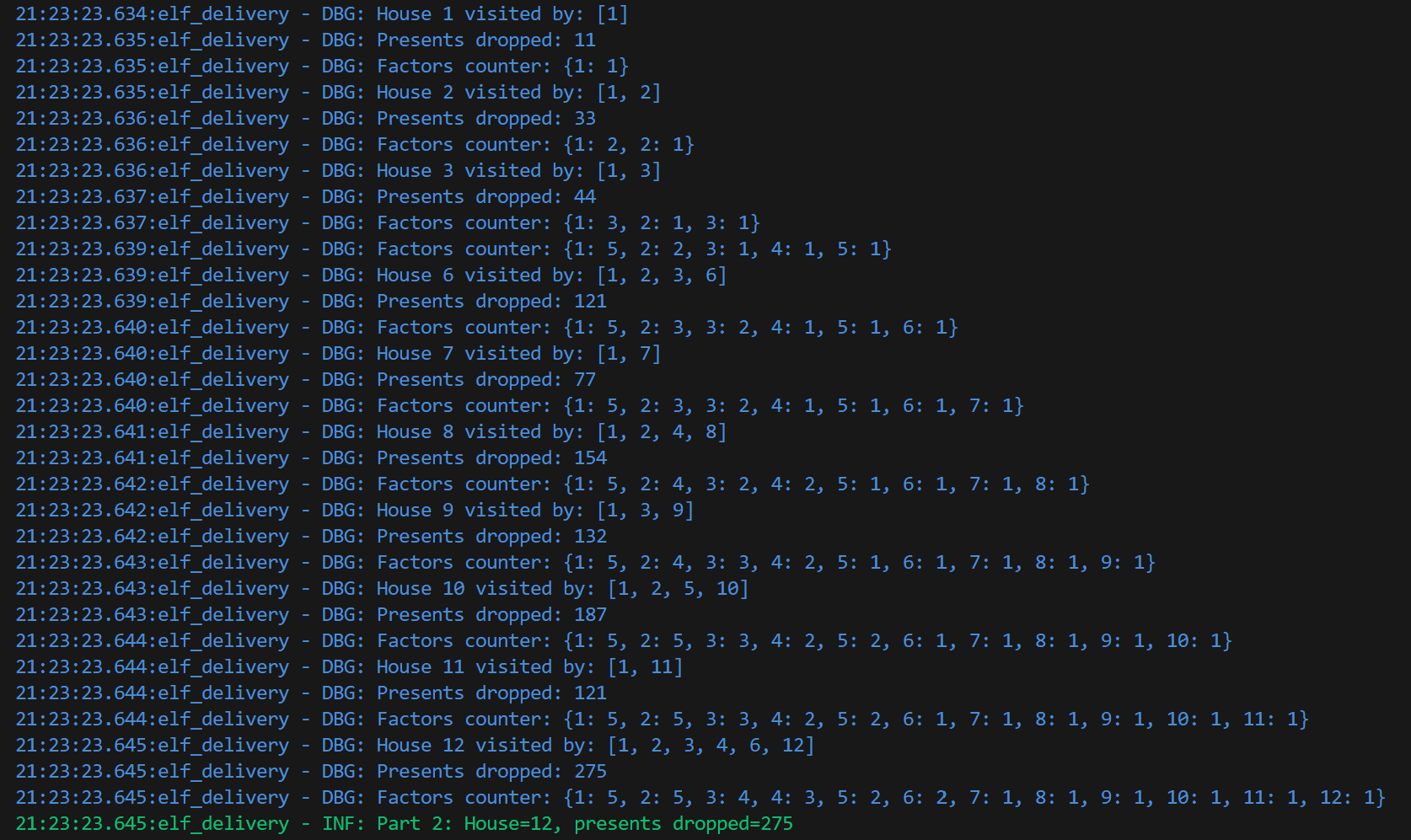
Elf drops, Part 2

With debugging enabled, note how each elf maxes out at 5 drops.

Results

With the real goal, this code takes quite a while to run. So I made an optimisation that halved the time!

I added the @lru_cache(maxsize=None) decorator to my get_factors() function. This is a built-in decorator, that comes with the functools module. It is a memoization mechanism that automatically caches the results of function executions, based on the arguments supplied. Because Part 1 and Part 2 both require calculation of factors for a huge number of houses starting at house 1, adding the lru_cache means that these factors are only ever calculated once for a given house. If we ask the function to calculate factors for a house that has been passed to the function before, then the result is automatically returned from the cache, rather than being recalculated! This is very efficient.

We add the cache by adding just one line, like this:

@lru_cache(maxsize=None)
def get_factors(num: int) -> set[int]:
    """ Gets the factors for a given number. Returns a set[int] of factors. 
        # E.g. when num=8, factors will be 1, 2, 4, 8 """
    factors = set()

    # Iterate from 1 to sqrt of 8,  
    # since a larger factor of num must be a multiple of a smaller factor already checked
    for i in range(1, int(num**0.5) + 1):  # e.g. with num=8, this is range(1, 3)
        if num % i == 0: # if it is a factor, then dividing num by it will yield no remainder
            factors.add(i)  # e.g. 1, 2
            factors.add(num//i)  # i.e. 8//1 = 8, 8//2 = 4
    
    return factors

Without cache:

35:14.794:elf_delivery - INF: Part 1: House=831600, presents dropped=36902400
35:38.804:elf_delivery - INF: Part 2: House=884520, presents dropped=36191925
35:38.816:elf_delivery - INF: Execution time: 44.948 seconds

With cache:

36:06.963:elf_delivery - INF: Part 1: House=831600, presents dropped=36902400
36:10.792:elf_delivery - INF: Part 2: House=884520, presents dropped=36191925
36:10.802:elf_delivery - INF: Execution time: 26.478 seconds

Cool, right?

‹›

Learning Python with Advent of Code Walkthroughs